5._Testing_Asymmetric_Encryption

Testing Asymmetric Encryption in a
Sustainable Hacking Lab

Michael Dorin

mike.dorin@stthomas.edu

https://orcid.org/0000-0002-5798-0623

University of St. Thomas, St. Paul, MN. USA

Sergio Montenegro

sergio.montenegro@uni-wuerzburg.de

https://orcid.org/0000-0002-3958-3018

Julius-Maximilians-Universität Würzburg, Würzburg Germany

Received: April 15th, 2024 / Accepted: May 18th, 2024

doi: https://doi.org/10.26439/interfases2024.n19.7058

ABSTRACT. The Aerospace Information Technology Department (Computer Science VIII) at University of Würzburg explores many facets of aerospace systems, including secure telemetry and telecommand systems. Because satellites are expensive and indispensable, thorough protection and security research is necessary. Security algorithms are often processor-intensive, which can deprive payload applications of valuable execution cycles and even system power, thus making proper algorithm selection essential. A mechanism for execution and analysis on devices of similar capability to hardware systems used in space applications is essential for proper algorithm selection. This paper shows that it is possible to create an inexpensive and sustainable lab to efficiently and correctly test encryption algorithms and protocols using discarded tablet computers and inexpensive single-board computers. The lab constructed began by evaluating three public encryption key algorithms to assess computational space and time requirements. The three algorithms include an implementation of prime number-based Rivest-Shamir-Adleman (RSA) and two elliptic-curve cryptography-based key-exchange implementations. The initial results for the three algorithms show RSA memory requirements are not substantially different from the elliptic curve algorithms, but running times are comparatively slower. The first elliptic curve cryptography algorithm has moderate run time and space requirements, while the second one shows an improved run time but requires more space. This study reveals that testing algorithms using affordable lab devices can provide useful performance related data.

Keywords: asymmetric encryption / sustainable hacking lab / satellite communications / RODOS

RESUMEN. El Departamento de Tecnología de la Información Aeroespacial (Ciencias de la Computación VIII) de la Universidad de Würzburg explora muchos aspectos de los sistemas aeroespaciales, incluidos los sistemas seguros de telemetría y telemando. Debido a que los satélites son costosos e indispensables, es necesaria una investigación exhaustiva sobre su protección y seguridad. Los algoritmos de seguridad suelen requerir un uso intensivo de los procesadores, lo que puede privar a las aplicaciones de carga útil de ciclos de ejecución valiosos e incluso de energía del sistema. Por ello, es esencial una selección adecuada de los algoritmos que se utilizarán. Disponer de un mecanismo para la ejecución y el análisis, en dispositivos de capacidades similares a los sistemas y el hardware que se utilizan en las aplicaciones espaciales, es fundamental para una correcta selección de algoritmos. Este artículo muestra que es posible crear un laboratorio económico y sostenible para probar de manera eficiente y precisa los algoritmos de encriptación y protocolos utilizando tabletas descartadas y computadoras de placa única económicas. El laboratorio que se construyó con ellas se utilizó para evaluar tres algoritmos públicos de clave de encriptación para determinar los requisitos computacionales de espacio y tiempo. Los tres algoritmos incluyen una implementación del algoritmo de clave pública basado en números primos Rivest-Shamir-Adleman (RSA) y dos implementaciones de intercambio de clave basadas en criptografía de curva elíptica. Los resultados iniciales muestran que los requisitos de memoria de estos algoritmos no son sustancialmente diferentes, pero los tiempos de ejecución del algoritmo RSA son comparativamente más lentos. El primer algoritmo de criptografía de curva elíptica tiene requisitos moderados de tiempo de ejecución y espacio, mientras que el segundo muestra un tiempo de ejecución mejorado, pero requiere más espacio. Este estudio revela que probar algoritmos utilizando dispositivos de laboratorio asequibles puede proporcionar datos útiles acerca de su rendimiento.

PALABRAS CLAVE: encriptación asimétrica / laboratorio de hackeo sostenible / comunicaciones satelitales / RODOS

1. INTRODUCTION

The negative perception of hacking involves illicitly accessing computer systems and data (Sciglimpaglia Jr, 1991). Cybercriminals can use hacking to sabotage scientific and aerospace endeavors, hamper studies, breach security and endanger missions. Although researchers from the Aerospace Information Technology Department (Computer Science VIII) at the University of Würzburg have yet to encounter any security issues related to commanding spacecraft, as the cost of powerful hardware systems decreases, so does the cost of cyberattacks. This makes it necessary to build a hacking lab to start evaluating encryption algorithms.

Many researchers utilize virtual machines (VM) to create security labs. For example, Guarda et al. (2016) describe penetration testing using virtual environments, while Lee et al. (2023) describe simulation-based cybersecurity testing. As early as 2003, Garfinkel and Rosenblum (2003) were able to demonstrate a successful use of virtual machines for intrusion detection. VMs can work satisfactorily in many environments; however, since resources are shared overall, multiple VMs can create confusing time measurements when running different tests.

In regards to encryption algorithms, several papers in the current literature address encryption and telemetry/telecommand system (TM/TC) security. For example, López and Fraga (2016) describe a TM/TC encryption system using the Advanced Encryption Standard (AES). This paper suggests that AES is emerging as the new de-facto standard for satellite telemetry and telecommand systems. Another interesting paper on TM/TC security is from Hoang et al. This compelling paper discusses physical layer security (Hoang et al., 2021). Meanwhile, Herpel et al. (2016) address security by showing a software architecture for satellites. While these papers are helpful, they do not specifically address algorithms that are a good fit for the Realtime Onboard Dependable Operating System (RODOS). More information on RODOS can be found in Appendix A.

Regarding algorithms appropriate for RODOS, further examination of the literature covers more specific algorithm implementations. Many papers discuss the efficient implementation of Rivest-Shamir Adleman (RSA). Two examples from Nozaki et al. (2001) and Zhou and Tang. (2011) offer detailed analyses. There are also several papers on the implementation of elliptic curve cryptography (ECC). Point operations, for instance, can also be partially reduced by using the Hamming weight of the private key (commonly known as the multiplicand ‘k’). In their work Fast Algorithms for Common-Multiplicand Multiplication and Exponentiation by Performing Complements, Chang et al. (2003) explain how to reduce the Hamming weight of the multiplicand which, in this case, can reduce point operations. Hamming weights have been discussed for more than fifty years and more information can be found in the work of Hamming (1970). Further research on using Hamming weights to save processing time has been conducted by various authors, including Kodali and Budwal (2013) and Huang et al (2010). Although these papers are interesting, they do not cover implementation details required by small devices.

Because previous research has not thoroughly addressed the security and encryption testing needs required for embedded applications in space using RODOS, this project explores the construction of a practical hacking lab to test the time it takes each of three asymmetric encryption algorithms to perform key exchange. This project selected specific RSA and ECC implementations having equivalent security levels when measured against symmetric encryption algorithms. In symmetric algorithms, if an n-bit key does not allow a faster attack than a brute force attack, then the algorithm is defined to have security level n (Lenstra, 2006). For this research, 80 bits of asymmetric encryption was determined to be the minimum acceptable level. RSA and ECC were selected to be compared at symmetric encryption levels of 80, 112, 128, 192 and 256 bits to evaluate algorithm performance. As such, corresponding RSA implementations of 1024, 2048, 3072, 7680 and 15360 bits were evaluated, while the corresponding curves B163, B233, B283, B409 and B571 were selected for ECC testing (Brown et al., 2001). Algorithms ECC were implemented in C using an embedded ECC library (Kokke, 2017). Algorithms for RSA were also implemented in C and a large number library (BigDigits multiple-precision arithmetic source code, s/f). This paper demonstrates that creating a hacking lab and testing algorithms for ground, air and space communications is feasible and practical.

2. PROJECT FOUNDATION AND ALGORITHMS

2.1 TM/TC and RODOS

Every satellite and spacecraft requires telemetry and command interfaces at one or more ground stations to receive payload data and to monitor and control the spacecraft. Telemetry (TM) refers to the process of collecting and transmitting data from the spacecraft to the ground station, where this data is visualized for operators and engineers. Telecommand (TC) interfaces allow operators to send commands and instructions from the ground station to the spacecraft (Maral et al., 2020).

Typically, TM and TC are developed separately, with one team developing the TM software for the spacecraft side and another team developing the TC counterpart for the ground station. However, RODOS employs an application generator called Corfu to specify telemetry and telecommands. Corfu generates the code for the spacecraft and for the ground station. For the spacecraft, it generates the distribution of telecommands and a frame to interpret and execute each of them, while for TM it generates the frame to collect, pack and send data from the spacecraft to ground station. For the ground station side, Corfu generates decoders and graphical representations for all telemetry data. It generates buttons to send commands and fields to enter their parameters. These commands and their parameters are then encoded and sent to the spacecraft.

2.2. Encryption Algorithms Tested

Saltzer and Schroeder (1975) suggested that security mechanisms should be as small as possible to be of aid in their verification, which is undoubtedly true in resource-starved environments. To allow for the creation of small mechanisms and achieve secure communication, a practical hacking lab was built, and RSA plus two variations of ECC were tested.

2.2.1 Rivest-Shamir-Adleman

The first algorithm tested was an RSA public key authentication. RSA was invented in 1977 and is based on the difficulty of factoring large composite numbers into their prime factors. The algorithm relies on a public-private key pair, where the public key is used for encryption and the private key is used for decryption (Salami et al., 2023). More basic information on RSA can be found in Appendix B. For this test, a complete RSA key exchange was simulated. RSA was selected for this test because of its perceived compactness and simplicity of implementation.

2.2.2 Elliptic Curve Cryptography

This paper does not describe the details of ECC, but information is provided in Appendix C. Two variants of ECC multiply were evaluated simulating a key exchange using Elliptic Curve Diffie-Helman (ECDH). More information on ECDH can be found in Appendix D. The first variant employs the hamming weight of the multiplicand to potentially reduce the overall number of operations required for the multiply. The second approach also employs Hamming weights, but in this variant an entry in the lookup table is created for each bit of the curve. For example, in the case of the 163-bit curve, 163 entries are created. As with standard multiplication, the private key ‘k’ is shifted to the right. However, instead of doing a ‘double and add’ when odd, the point value for the particular bit is found in the lookup table and is then added to a running sum, creating the product. This eliminates the need for the point to double each pass through the loop. As before, this algorithm can potentially be made even faster using Hamming weights. To take advantage of Hamming weights, an inverse value of k, inverseK, is subtracted from the next power of two above k, np. The resulting calculation is

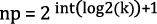
The value of inverseK is calculated by subtracting k from the next power, as

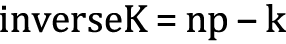
Next, choose k or inverseK based on the Hamming weight. If inverseK is used, an extra subtraction is done at the end to transform the result to the original k, but the algorithm guarantees that the number of adds required is never greater than the number of bits in k, though there is the Hamming math at the beginning and a point subtract required at the end when inverseK is used. Source code for this algorithm is provided in Appendix E. The algorithm demonstrated here is a refinement of the implementation made by Dorin (2009) and was inspired by work conducted in the 1960s when speeding up normal multiplication was required. For instance, Mitchell (1962) described computer multiplication and division using binary logarithms. More recently, Koshelev (2024) describes using Hamming weight for elliptic curve hashing algorithms. Nascimento et al. (2015) describe the use of lookup tables in their 8-bit implementation of ECC.

2.3 Simulation Equipment

Establishing a sustainable hacking lab requires completing common steps regardless of the algorithms being tested. The first action was acquiring suitable devices. For this study, both Linux-based devices and single-board computers were desired. Regarding Linux-based devices, systems were recommended to have at least 4 GB of RAM and at least 20 GB of persistent storage (The Linux Mint Team, 2024a). It was not difficult to find suitable devices as many surplus devices are sold on eBay for less than USD20 each. The final tablets arrived in the form of a collection of electronics generously donated to the University of St. Thomas. Those planning to set up an analogous lab can likely find equipment by contacting local electronics recyclers. Discarded electronics are often available at a low price or even at no cost. Recycling electronics can save money and increase the sustainability of the lab’s construction. Specifications for the selected are available in Table 1. An image of a selected tablet is shown in Figure 1.

Table 1

Tablet specifications

Component	Details
CPU Frequency	1.4 Gigahertz
Processor Type	Intel Atom (Quad-Core)
Available Networking	Wi-Fi and Bluetooth
USB Ports	1 External (3 total)
Available RAM	4 Gigabytes
Persistent Storage	30 Gigabytes
Operating System	Linux (Mint)

The STM32F407-DISC1 was selected given that an actual embedded target was also desired for this project. According to the manufacturer, the STM32F407VGT6 microcontroller features a 32-bit Arm Cortex-M4 with an FPU core, 1-MB of Flash memory, and 192 KB of RAM (STMicroelectronics, 2024a). See Figure 2.

The tablets were re-imaged with the Mint distribution of the Linux operating system (The Linux Mint Team, 2024b). Mint was selected because it is stable, well-supported and easy to install. GNU compiler collection (GCC) tools were used for development on the Linux devices (Fenlason & Stallman, 1998). The STM32 Discovery board was used as-is out of the box. The STM32CubeIDE was used for development and project generation (STMicroelectronics, 2024b). Standard settings given by the STM32CubeIDE were not modified.

Figure 1

The tablet device used for testing.

Figure 2

The STM32 discovery board used in testing

3. RESULTS

On each hardware platform, key-exchange mathematics were performed on the algorithm being tested. This test code was executed continuously on the STM32 and an oscilloscope was used to measure timing. The key value used in the exchange remained unchanged for all tests. Table 2 displays a summary of results for the minimally acceptable security level, equivalent to 80 bits symmetric encryption, on both platforms.

Table 2

Program response time for 80 bit security strength

Device	Build	Test Program Size (bytes)	Response Time (msec.)
STM32	RSA	37,980	3,810
STM32	ECDH Hamming Only	28,072	2,730
STM32	ECDH Hamming and Lookup Table	37,296	2,095
Linux	RSA	77,904	184.45
Linux	ECDH Hamming Only	36,776	46.13
Linux	ECC Hamming and Lookup Table	37,664	31.49

3.1 RSA

The first algorithm tested was RSA, using the STM device. Table 3 shows the required time for completion as well as the size of the executable. Note that the terms text, data, and bss refer to different sections of program memory. The text section contains executable code. The bss section contains uninitialized variables. The data section contains global and static variables (Pesch et al., 1993). Table 3 reports the STM32 results, Table 4 reports the results from the Linux system.

Table 3

RSA key exchange simulation (STM32)

Security Strength	RSA bits	Program Size Bytes (text, data, bss)	Response Time (msec)
80	1024	35,228 bytes	3,810
112	2048	38,848 bytes	27,970
128	3072	39,360 bytes	90,400
192	7680	41,664 bytes	844,926*
256	15360	45,504 bytes	3,824,620*

Note. * indicates that operation time is estimated.

Table 4

RSA key exchange simulation (Linux)

Security Strength	RSA bits	Program Size Bytes (a.out)	Response Time (msec)
80	1024	77,904 bytes	184.45
112	2048	77,904 bytes	1,350.69
128	3072	82,000 bytes	4,399.72
192	7680	82,000 bytes	65,894.26
256	15360	86,096 bytes	516,835.02

3.2 ECDH Using Basic Multiply with Hamming Weight

The next algorithm tested was ECDH using ECC basic multiply with Hamming weight. This version of multiplication did not use a lookup table. STM32 results are shown in Table 5, the Linux results are shown in Table 6.

Table 5

ECDH key exchange simulation (No lookup) (STM32)

Security Strength	ECC Algorithm	Program Size Bytes (text, data, bss)	Response Time (msec)
80	B163	28,156	312.94
112	B233	28,176	545.0
128	B283	28,192	720.0
192	B409	28,228	1,475.0
256	B571	28,244	2,570.0

Table 6

ECDH key exchange simulation (No lookup) (Linux)

Security Strength	ECC Algorithm	Program Size Bytes (a.out)	Response Time (msec)
80	B163	36,776	46.13
112	B233	36,800	84.5
128	B283	36,800	113.11
192	B409	36,816	232.17
256	B571	36,840	444.39

3.3 ECDH Using Basic Multiply with Hamming Weight and Lookup Table

The final algorithm tested was ECDH using ECC basic multiply with Hamming weight and lookup table. Table 7 reports STM32 results, Table 8 shows results with the Linux system.

Table 7

ECDH key exchange simulation (Lookup Table) (STM32)

Security Strength	ECC Algorithm	Program Size Bytes (text, data, bss)	Response Time (msec)
80	B163	37,012	214.78
112	B233	44,492	372.3
128	B283	48,872	495.38
192	B409	71,464	1,005.0
256	B571	111,224	1,755.0

Table 8

ECDH key exchange simulation (Lookup Table) (Linux)

Security Strength	ECC Algorithm	Program Size Bytes (a.out)	Response Time (msec)
80	B163	37,664	31.49
112	B233	44,832	58.25
128	B283	49,184	78.44
192	B409	75,808	156.57
256	B571	119,584	306.92

3.4 Power Consumption

Power consumption was measured during all of the tests. On Linux, irrespective of algorithm, PowerTOP (Zeitouny & Akturan, 2013) estimated 1.53 Watts of power consumption and 100 % CPU utilization. On the STM-32 device, it was possible to measure power usage by putting a meter in-line with the power supply. Power consumption varied between 47.3 mA and 52.9 mA. STM32 Results are shown in Table 9.

Table 9

Power consumption STM32

Security Strength	ECC – No lookup (mA.)	ECC – Lookup (mA.)	RSA (mA.)
80	47.3	47.4	52.9
112	47.0	46.9	51.0
128	47.5	47.3	49.4
192	47.5	47.5	NA
256	47.3	47.8	NA

Setting up the lab hardware was trouble-free, but future work may require performance tuning of the STM32 board. Setting up the development systems for the STM32 board and the Linux system went smoothly. While the STM32 and Linux device did run all the required applications, the STM32 required substantial time to process large numbers. It was necessary to use quadratic regression to estimate response times for RSA-7680 and RSA-15360.

When it came to space requirements, the RSA algorithm was expected to be the best choice given that the basic algorithm is comparatively uncomplicated. However, the ECC B163 algorithm without a lookup table turned out to be the best choice in terms of space. This was due to the space required by the large integer math routines needed for implementation. Hamming ECC with lookup table multiply demanded the most space, with ECC multiply without the lookup table falling in between.

Considering the required time per operation, ECC using Adaptive Hamming with lookup was the fastest of all three algorithms. Calculations were approximately 30 % faster than tests ran without the lookup table on both the STM32 and Linux boards. RSA was the slowest. ECDH with basic ECC multiply again fell in between. Both elliptic curve algorithms were faster than the equivalent RSA algorithm for all tests.

In terms of power, there does appear to be a small advantage for using ECC algorithms instead of traditional RSA. However, this advantage is marginal and warrants further exploration.

4. CONCLUSIONS

This research had multiple goals. The first goal was to determine whether it is possible to create a practical hacking lab to test security algorithms and provide quality data at an affordable price. While validating the first goal, a second goal was established to measure different asymmetric encryption algorithms using the aforementioned hacking lab. To this end, a hacking lab was created from STM32 boards and discarded tablet PCs. The selected devices ran the necessary software and performed tests on RSA and two variants of ECC multiple encryption algorithms.

Developing this hacking lab shows that a practical, inexpensive and sustainable solution for enhancing security in aerospace environments is possible. Several avenues for further research are now open. For instance, formally testing key exchanges and synchronous algorithms could prove essential for future projects. In addition, testing block versus streaming ciphers for applications specific to RODOS TM/TC could also prove fruitful. Finally, further research could be directed toward refining the testing procedures and expanding the scope of the lab’s capabilities. The results demonstrated in this project indicate a promising future for research on hacking labs.

5 Appendices

Appendix A: RODOS

Realtime Onboard Dependable Operating System (RODOS) is a real-time operating system for embedded systems. It was designed for space applications but is suitable for any application demanding high dependability. An important feature of RODOS is its integrated real-time middleware. Developing the control and payload software on top of middleware provides maximum modularity for developers. Applications/modules can be developed independently and can be easily swapped without worrying about side effects since all modules are encapsulated as Building Blocks (BB) and can be accessed by other resources and access other resources through well-defined interfaces.

RODOS was implemented as a software framework in C++ with an object-oriented application interface. It is organized into layers: the lowest layer (1) is responsible for controlling the embedded system hardware (HAL: Hardware abstraction layer). The next layer (2), the kernel, administers local resources, threads and time. On top of the kernel is the middleware (layer 3), which enables communication between BBs using a publisher-subscribe multicast protocol. On top of the middleware sit user-implemented applications (layer 4), which are distributed software networks of simple BBs. The BBs API on the top of the middleware is a service-oriented interface. BBs interact by providing services to other BBs and using services from other BBs.

RODOS can be executed on different hardware platforms (arm, PPC, X86, Spark, Leon) and on top of Linux or Posix operating systems. It is possible to test and simulate target applications on various devices using RODOS on top of Linux.

Appendix B: Rivest-Shamir-Adleman (RSA)

RSA encryption is used to secure data transmission, employing a public key for encryption and a private key for decryption. Using the public key, anyone can encrypt a message. However, the private key is required to decipher them.

Key generation

1. Choose two large prime numbers, p and q

2. Compute their product, n = pq, which becomes the modulus for both keys.

3. Calculate the totient function ϕ(n) = (p − 1)(q − 1).

4. Choose an integer e such that 1 < e < ϕ(n) and gcd(e, ϕ(n)) = 1. This becomes the public exponent.

5. Compute the modular inverse of e modulo ϕ(n) to get d, which is the private exponent.

To encrypt a message M, compute C ≡ Me mod n.
To decrypt the ciphertext C, compute M ≡ Cd mod n.

RSA’s security relies on the difficulty of factoring the modulus n into its prime factors. As long as the prime factors p and q are sufficiently large, factoring n and breaking the RSA encryption is computationally infeasible (Salami et al., 2023).

Appendix C: Elliptic Curve Cryptography

Elliptic Curve Cryptography (ECC) is a means of performing asymmetric encryption with faster processing times than other algorithms. ECC leverages the properties of elliptic curves over finite fields and can be used to provide encryption and create digital signatures. An advantage to ECC is the ability to offer equivalent security to traditional cryptographic algorithms like RSA albeit with smaller key sizes, making it more efficient for resource-constrained environments. Elliptic curves used in ECC are defined by equations of the form y2 = x3 + ax + b., where a and b are coefficients chosen based on specific mathematical properties. These curves exhibit various properties, including having a group structure defined by point addition and scalar multiplication (Edoh, 2004).

The simplest form of point multiplication is commonly called “the double and add method” and is almost effortless to implement (Eisentraeger et al., 2002). Algorithm 1 below illustrates how to multiply the scalar value k by a specific point on the curve, P.

Input: Scalar multiplier k, point P

Output: Resultant point Q = kP

Set Q = Φ ; // point-at-infinity

while (k ̸= 0) do

if (k is odd) then

Q = Q + P;

end

P = 2P;

k = k/2;

end

return Q;

The scalar k is shifted right for each iteration through the loop. Whenever bit zero of k is one, the current point value is added to the output. The point value P is doubled during each pass through the loop until k is zero, when the point Q is returned (Eisentraeger et al., 2002; Anoop, 2007).

Appendix D: Elliptic Curve Diffie-Helman (ECDH) Algorithm

1. Alice selects a (secret) random natural number a, calculates P = a * G. P is sent to Bob.

a is Alice’s private key.

P is Alice’s public key.

2. Bob selects a (secret) random natural number b, calculates Q = b * G. Q is sent to Alice.

b is Bob’s private key.

Q is Bob’s public key.

3. Alice calculates S = a * Q = a * (b * G).

4. Bob calculates T = b * P = b * (a * G).

T = S = the new shared secret.

More information can be found in RFC4492 (Blake-Wilson et al., 2006)

and Kokke (2017).

Appendix E: Elliptic Curve Example Source Code

#include “ecdh.h”

void gf2point_hamming_and_lookup_mutliply(gf2elem_t x,

gf2elem_t y, const scalar_t exp)

{

scalar_t one = {1}; //scalar value one, used for shifting

scalar_t nextPowerOfTwoAbove = {0};

scalar_t result = {0};

int numberofHighestOneBit;

numberofHighestOneBit = bitvec_degree(exp);

/* bitvec_degree holds number of the highest one-bit + 1 */

bitvec_lshift(nextPowerOfTwoAbove, one, numberofHighestOneBit );

int hammingWeight = hamming_weight(exp);

bigint_subtract(result, nextPowerOfTwoAbove, exp);

int hammingWight2 = hamming_weight(result);

if (hammingWeight < hammingWight2) {

gf2point_multiply_with_lookup(x, y, exp);

} else {

gf2point_multiply_with_lookup(x, y, result );

gf2field_add(y,x,y );

gf2point_add(x, y, Tx[numberofHighestOneBit+1],

Ty[numberofHighestOneBit+1]);

}

void gf2point_multiply_with_lookup(gf2elem_t x, gf2elem_t y,

const scalar_t exp)

{

int index = 0;

int currentBit = 0x1;

int currentByte = 0;

for (index = 1; index < ECC_PRV_KEY_SIZE * 8; index++) {

if (exp[currentByte] & currentBit) {

gf2point_add(x, y,Tx[index], Ty[index]);

}

currentBit =currentBit << 1;

if (currentBit == 0x00000000)

{

currentBit = 0x1;

currentByte+=1;

}

Note. Requires tiny-ECDH-c from Kokke (2017).

REFERENCES

Anoop, M. S. (2007). Elliptic curve cryptography. An implementation guide. https://informatika.stei.itb.ac.id/~rinaldi.munir/Kriptografi/2014-2015/ECC_Tut_v1_0.pdf

BigDigits multiple-precision arithmetic source code (s/f). DI Management. https://www.di-mgt.com.au/bigdigits.html

Blake-Wilson, S., Nystrom, M., Hopwood, D., Mikkelsen, J. & Wright, T. (2006). Network working group. https://www.rfc-editor.org/pdfrfc/rfc4366.txt.pdf

Brown, M., Hankerson, D., López, J. & Menezes, A. (2001). Software implementation of the NIST elliptic curves over prime fields. In D. Naccache (Ed.), Topics in Cryptology — CT-RSA 2001. (pp. 250-265). Springer. https://doi.org/10.1007/3-540-45353-9_19

Chang, C-C., Kuo, Y-T. & Lin, C-H. (2003). Fast algorithms for common-multiplicand multiplication and exponentiation by performing complements. Proceedings 17th International Conference on Advanced Information Networking and Applications (AINA) (pp. 807-811). IEEE Computer Society. https://doi.org/10.1109/AINA.2003.1193005

Dorin, M. (2009). Implementation of standards based public key cryptography for small processor based systems [Master’s thesis] Metropolitan State University, St. Paul, Minnesota.

Edoh, K. D. (2004). Elliptic curve cryptography: Java implementation. Proceedings of the 1st Annual Conference on Information Security Curriculum Development (pp. 88-93). Association for Computing Machinery. https://doi.org/10.1145/1059524.1059542

Eisentraeger, K., Lauter, K. & Montgomery, P. L. (2002). An efficient procedure to double and add points on an elliptic curve. Cryptology ePrint Archive, paper 2002/112. https://eprint.iacr.org/2002/112.

Fenlason, J. & Stallman, R. (1998). The GNU Profiler. https://ftp.gnu.org/old-gnu/Manuals/gprof-2.9.1/html_mono/gprof.html

Garfinkel, T. & Rosenblum, M. (2003). A virtual machine introspection based architecture for intrusion detection. Network and Distributed System Security Symposium, 3. https://suif.stanford.edu/papers/vmi-ndss03.pdf

Guarda, T., Orozco, W., Augusto, M. F., Morillo, G., Arévalo Navarrete, S. & Mota Pinto, F. (2016). Penetration testing on virtual environments. In: Proceedings of the 4th International Conference on Information and Network Security (ICINS ’16) (pp. 9-12). https://doi.org/10.1145/3026724.3026728

Hamming, R. W. (1970). On the distribution of numbers. Bell System Technical Journal, 49(8), 1609-1625. https://doi.org/10.1002/j.1538-7305.1970.tb04281.x

Herpel, H-J., Kerep, M., Montano, G., Eckstein, K., Schön, M. & Krutak, A. (2016). MILS compliant software architecture for satellites. MILS@HiPEAC. https://core.ac.uk/download/pdf/144785917.pdf

Hoang, T. M., Duong, T. Q., Tuan, H. D., Lambotharan, S. & Hanzo, L. (2021). Physical layer security: detection of active eavesdropping attacks by support vector machines. IEEE Access, 9, 31595-31607. https://doi.org/10.1109/ACCESS.2021.3059648

Huang, X., Shah, P. G. & Sharma, D. (2010). Minimizing hamming weight based on 1’s complement of binary numbers over GF (2m)). 12th International Conference on Advanced Communication Technology (ICACT), 1226-1230. https://researchsystem.canberra.edu.au/ws/portalfiles/portal/28927012/full_text_published_15.pdf

Kodali, R. K. & Budwal, H. S. (2013). High performance scalar multiplication for ECC. 2013 International Conference on Computer Communication and Informatics (pp. 1-4). https://doi.org/10.1109/ICCCI.2013.6466286

Kokke. (2017). Small and portable implementation of ECDH in C. https://github.com/kokke/tiny-ECDH-c

Koshelev, D. (2024), Some remarks on how to hash faster onto elliptic curves. Journal of Computer Virology and Hacking Techniques. (2024). https://doi.org/10.1007/s11416-024-00514-4

Lee, D. H., Kim, C. M., Song, H. S., Lee, Y. H. & Chung, W. S. (2023). Simulation-based cybersecurity testing and evaluation method for connected car V2X application using virtual machine. Sensors, 23(3), 1421. https://doi.org/10.3390/s23031421

Lenstra, A. (2006). Key lengths contribution to the handbook of information security. https://blkcipher.pl/assets/pdfs/NPDF-32.pdf

López, D. & Fraga, E. (2016). Tm/tc encryption system. In: 14th International Conference on Space Operations, Article 2330. American Institute of Aeronautics and Astronautics. https://arc.aiaa.org/doi/10.2514/6.2016-2330

Maral, G., Bousquet, M. & Sun, Z. (2020). Satellite communications systems: systems, techniques and technology. Wiley.

Mitchell, J. N. (1962). Computer multiplication and division using binary logarithms. IRE Transactions on Electronic Computers, EC-11(4), 512–517. https://doi.org/10.1109/TEC.1962.5219391

Nascimento, E., López, J. & Dahab, R. (2015). Efficient and secure elliptic curve cryptography for 8-bit AVR microcontrollers. In R. Chakraborty, P. Schwabe & J. Solworth (Eds.) Security, privacy and applied cryptography engineering. Lecture notes in computer science, 9354, pp. 289-309. Springer. https://doi.org/10.1007/978-3-319-24126-5_17

Nozaki, H., Motoyama, M., Shimbo, A. & Kawamura, S. (2001). Implementation of RSA algorithm based on RNS Montgomery multiplication. In C. K. Koc, D. Naccache & C. Paar (Eds.), Cryptographic hardware and embedded systems—CHES 2001. Lecture Notes in Computer Science, 2162, 364-376. Springer. https://doi.org/10.1007/3-540-44709-1_30

Opus IVS. (2024). Opus IVS.About Us https://www.opusivs.com/about/

Pesch, R. H., Osier, J. M. & Support, C. (1993). The Gnu binary utilities. https://web.mit.edu/gnu/doc/html/binutils_toc.html

Salami, Y., Khajehvand, V. & Zeinali, E. (2023). Cryptographic algorithms: a review of the literature, weaknesses and open challenges. Journal of Computer & Robotics, 16(2), 63-115. https://doi.org/10.22094/jcr.2023.1983496.1298

Saltzer, J. H. & Schroeder, M. D. (1975). The protection of information in computer systems. Proceedings of the IEEE, 63(9), 1278–1308. https://doi.org/10.1109/PROC.1975.9939

Sciglimpaglia Jr., R. J. (1991). Computer hacking: a global offense. Pace International Law Review, 3(1), 204-266. https://doi.org/10.58948/2331-3536.1020

STMicroelectronics. (2024a). STM32F4DISCOVERY - Discovery kit with STM32F407VG MCU. https://www.st.com/en/evaluation-tools/stm32f4discovery.html

STMicroelectronics. (2024b). STM32CubeIDE - Integrated development environment for STM32. https://www.st.com/en/development-tools/stm32cubeide.html

The Linux Mint Team. (2024a), Linux Mint - FAQ. Linux Mark Institute. https://linuxmint.com/faq.php

The Linux Mint Team. (2024b), Linux Mint - Download. Linux Mark Institute. https://www.linuxmint.com/download.php

Zeitouny, C. & Akturan, C. (2013). Linux* power efficiency analysis methods. A look at power efficiency analysis methods under Linux environments. Intel corporation. https://www.intel.com/content/dam/develop/external/us/en/documents/linux-power-efficiency-analysis-methods-2.pdf

Zhou, X. & Tang, X. (2011). Research and implementation of RSA algorithm for encryption and decryption. Proceedings of 2011 6th international forum on strategic technology (pp. 1118-1121). https://doi.org/10.1109/IFOST.2011.6021216