Gestión de inventarios de una compañía
importadora de repuestos de transmisión
de potencia de maquinaria pesada
Mateo Núñez-Oviedo
https://orcid.org/0009-0008-2611-669X
Departamento de Ingeniería Industrial, Universidad de los Andes,
Bogotá, Colombia
Luis Tarazona-Torres*
https://orcid.org/0000-0003-0567-6926
Departamento de Ingeniería Industrial, Universidad de los Andes,
Bogotá, Colombia
Recibido: 15 de mayo del 2024 / Aceptado: 13 de junio del 2024
Publicado: 12 de diciembre del 2024
doi: https://doi.org/10.26439/ing.ind2024.n47.7116
RESUMEN. Este estudio tuvo como objetivo hacer un análisis de la gestión de inventarios de una compañía importadora de repuestos de transmisión de potencia. La investigación fue del tipo aplicado, con diseño no experimental, alcance descriptivo y enfoque cuantitativo. Se tomó como caso una empresa importadora de productos desde China. Se evaluaron escenarios determinísticos y estocásticos comparándolos con el escenario actual de la empresa, y se aplicaron métodos relacionados con cada escenario, considerando también el comportamiento de la demanda y haciendo un análisis de los modelos con pronósticos de esta. Se concluyó que el método estocástico, específicamente el modelo (S, T), ha resultado ser más rentable en comparación con el escenario actual y el determinístico, principalmente por la reducción de faltantes y la homogeneidad en el comportamiento del inventario.
PALABRAS CLAVE: control de inventarios / maquinaria / repuestos / transmisión de potencia / cadena de suministro / empresas / importación
Inventory Management for an Import Company of Power Transmission Spare Parts for Heavy Machinery
ABSTRACT. The aim of this study was to analyses the inventory management of a company that imports power transmission spare parts. The study was of the applied type, with a non-experimental design, descriptive scope, and quantitative approach. A company importing its products from China was taken as a case study. Deterministic and stochastic scenarios were evaluated in comparison with the company’s current scenario and methods related to each scenario were applied, also considering the behavior of demand, and analyzing the models with forecasts of these. It was concluded that the stochastic method, specifically the (S, T) model, has proved to be more profitable compared to the current scenario and the deterministic one, mainly due to the reduction of shortages and the homogeneity in the behavior of the inventory.
KEYWORDS: inventory control / machinery / spare parts / power transmission / supply chain / business enterprises / imports
Este estudio no fue financiado por ninguna entidad.
*Autor corresponsal.
Correos electrónicos en orden de aparición: m.nunezo@uniandes.edu.co; le.tarazona@uniandes.edu.co
Este es un artículo de acceso abierto, distribuido bajo los términos de la licencia Creative Commons Attribution 4.0 International (CC BY 4.0).
INTRODUCCIÓN
El sector global de repuestos para la transmisión de potencia, crucial para la operatividad de maquinaria industrial, depende en gran medida de importaciones, en especial, en mercados con complejos procesos aduaneros y regulaciones locales. Productores clave de Estados Unidos, Alemania, China, Japón e Italia dominan este mercado con productos como engranajes, correas y cadenas. En Colombia, la gestión de inventarios enfrenta desafíos significativos debido al uso de políticas empíricas que no consideran un análisis detallado de rotación de productos, lo que lleva a escasez o exceso de inventario, que afecta la eficiencia operativa y la capacidad de respuesta a la demanda del mercado (Chopra & Meindl, 2008).
La falta de métodos basados en pronósticos precisos conduce a decisiones arbitrarias sobre las cantidades que se deben pedir, generando ineficiencias, obsolescencia del producto y pérdida de valor comercial. Implementar políticas de inventario robustas que integren análisis de rotación y pronósticos precisos es crucial para mitigar estos problemas y fortalecer la operatividad empresarial.
En este contexto, la adopción de políticas como la cantidad económica de pedido (EOQ) y modelos como el de revisión continua Q, nR, y el de revisión periódica S, T, se presentan como soluciones eficaces. Estos métodos, diseñados para situaciones con demanda conocida o incierta, buscan optimizar los costos de gestión de inventarios y asegurar una cantidad adecuada de stock que satisfaga la demanda sin incurrir en costos excesivos de almacenamiento o escasez.
Ante esta problemática, es importante que las empresas de este sector consideren gestionar adecuadamente sus políticas de inventario, ya que podría tener repercusiones importantes en los costos asociados en la adquisición de los productos. Por eso, la presente investigación plantea la siguiente pregunta: ¿cómo determinar la política de inventario adecuada para minimizar costos totales anuales en la cadena de suministros de una empresa de repuestos de transmisión de potencia? Para dar una respuesta, se plantearon los siguientes objetivos de la investigación: (1) para un caso determinista, establecer la política de inventario que minimice los costos totales anuales; (2) definir pronósticos y aplicar la política debida; (3) en un caso estocástico, determinar la política de inventario que minimice los costos totales anuales; (4) realizar un análisis comparativo entre casos para determinar la mejor política según el tipo de producto.
A partir de la revisión de literatura realizada, se tiene que la gestión de inventarios es crucial para la eficiencia operativa y la rentabilidad en diversas industrias. Los modelos de inventario se clasifican en determinísticos y probabilísticos, adecuados para diferentes contextos. Según Nahmias (2007), los modelos determinísticos proporcionan predictibilidad y facilidad de gestión, mientras que los modelos probabilísticos ofrecen flexibilidad en entornos inciertos. Bai y Zhong (2008) señalan los retos de gestionar inventarios a nivel internacional, enfatizando la variabilidad de proveedores y las fluctuaciones de demanda. La revisión de González (2020) y de Parga-Prieto y Aranda-Pinilla (2018) sugiere el uso de técnicas heurísticas como Silver-Meal y Wagner-Whitin para adaptar los inventarios a cambios en mercados competitivos.
En sectores más específicos, la gestión de inventarios enfrenta desafíos únicos relacionados con la demanda estacional y la gestión de productos. Ardila (2010), Triana (2022), Martínez Arteaga (2016) y Rodríguez y Vidal (2009) discuten la importancia de métodos especializados para controlar eficazmente estos inventarios. La innovación y la mejora continua también son fundamentales en la gestión de inventarios. Alves et al. (2017) desarrollaron un algoritmo para controlar inventarios con demandas estocásticas, mejorando la optimización y la calidad del servicio. Ballou (2004) señala que las estrategias de inventarios deben alinearse con las metas del servicio al cliente, incluyendo pronósticos de demanda, programación de compras y decisiones de almacenamiento. Carvajal y Amaya (2011) propusieron un modelo mate-heurístico para mejorar la coordinación de inventarios bajo restricciones presupuestarias y de transporte compartido. Contreras Juárez et al. (2018) aplicaron el modelo EOQ y un modelo de revisión continua para demandas inciertas en la industria de la construcción, a fin de proporcionar soporte a las decisiones de niveles de inventarios y reducir costos operativos.
La gestión efectiva de inventarios es vital para garantizar la estabilidad financiera de las empresas. Restrepo et al. (2020) afirman que una gestión adecuada de inventarios es crucial para mantener la solvencia financiera. Monisola (2013) enfatiza la importancia de técnicas científicas y el uso de tecnologías de la información y comunicación (TIC) para una mejor toma de decisiones. Pérez Hualtibamba y Wong Aitken (2018) propusieron una metodología de gestión de inventarios basada en el análisis ABC, optimizando la cantidad económica de pedido, el punto de reorden y el número óptimo de pedidos, lo cual resultó en una reducción de costos y un aumento en la productividad. Rangel Vega (2016) también destacó la aplicación de modelos ABC y EOQ sin faltantes, mejorando el aprovechamiento de recursos y reduciendo costos operativos. Por otra parte, Gonçalves et al. (2020) se enfocan en el problema de dimensionamiento de stocks de seguridad e indican varios vacíos que afectan a su solución. También, Baron et al. (2017) subrayan la importancia de determinar un nivel óptimo de reorden s y un nivel de pedido S.
Respecto al uso de tecnologías de la información para la gestión moderna de inventarios, Arango et al. (2011), Guzmán-Camacho et al. (2014), Rojas Mancipe (2011) y Silva Gómez (2017) plantean la aplicación de estrategias de coordinación de inventarios gestionadas por el proveedor, además del uso de EDI (electronic data interchange) para mejorar las políticas de abastecimiento. Wiśniewski (2021) sugiere que la información sobre pronósticos debe ser accesible y gestionada en la nube, permitiendo actualizaciones en tiempo real. Esta revisión de literatura sugiere que la implementación de modelos avanzados de gestión de inventarios y tecnologías de la información puede mejorar significativamente la eficiencia operativa y la competitividad de las empresas, abordando las particularidades de diversos sectores y adaptándose a entornos inciertos.
METODOLOGÍA
La investigación utilizó un enfoque aplicado, no experimental, descriptivo y cuantitativo, centrado en una empresa que importa productos desde China e incluye una cadena de transmisión con 40 referencias distribuidas nacionalmente. La compañía enfrenta retos para mantener un nivel óptimo de inventario debido a una demanda variable, por lo que ha implementado revisiones mensuales de inventario para adaptarse a los bajos niveles, aunque el proceso de fabricación de las cadenas toma cerca de cuatro meses desde el pago anticipado. Los desafíos comprenden largos tiempos de entrega que, a veces, resultan en la superación del inventario disponible y agotamiento de productos. Es necesario mejorar la gestión de inventarios y explorar métodos más sofisticados para responder a la volatilidad de la demanda.
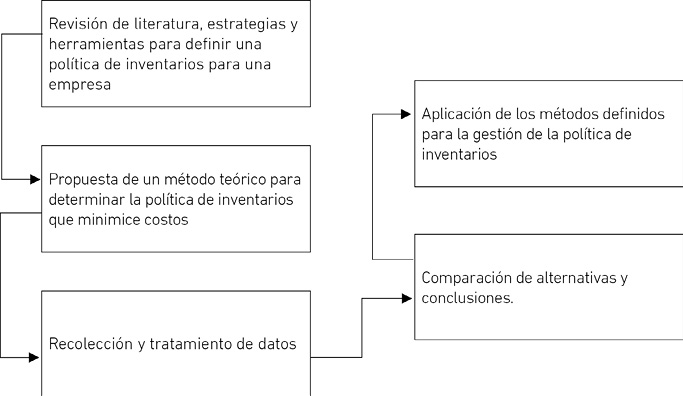
La investigación siguió un proceso estructurado, mostrado en la Figura 1, que comenzó con una revisión de literatura para explorar estrategias y herramientas existentes en la gestión de inventarios. Posteriormente, se propuso un método teórico para minimizar los costos de inventario y se llevó a cabo la recolección y tratamiento de datos necesarios para aplicar y validar este método. El proceso investigativo culminó en la aplicación práctica de los métodos definidos y una evaluación comparativa de estrategias para determinar la más eficiente y efectiva para la empresa. Este enfoque sistemático y basado en datos subraya la importancia de una planificación cuidadosa y adaptativa en la gestión de inventarios.
Figura 1
Procedimiento metodológico
La propuesta teórica para establecer una política de inventarios implica un análisis minucioso de variables clave, como la demanda de productos, costos logísticos y tiempos de entrega. Se examinan modelos teóricos existentes como el modelo de revisión continua (Q, R), heurísticas para el cálculo del tamaño de lote y el modelo de lote económico de pedido, adaptándolos a las particularidades del negocio, como la importación y la variabilidad de la demanda. La integración de técnicas de pronóstico y la implementación de modelos estocásticos y heurísticos mejoran la capacidad de prever la demanda futura. Establecer políticas de reorden y niveles de inventario apunta a optimizar los costos totales, incluyendo inventarios de seguridad para mitigar riesgos. Este enfoque teórico se valida mediante análisis de sensibilidad y simulaciones, permitiendo ajustes continuos para responder a variaciones en la demanda y condiciones del mercado, en busca de la mejora continua en la eficiencia de la gestión de inventarios.
El análisis de los costos actuales de la compañía abarca un periodo de 21 meses desde enero del 2022 hasta septiembre del 2023, tiempo en el que se realizaron cuatro importaciones con intervalos variados. Esta variabilidad complica la determinación de cantidades óptimas para satisfacer la demanda del mercado. Además, la retención prolongada de mercancía implica costos adicionales de almacenamiento, estimados en un 2 % del inventario, incluyendo costos de capital y almacenamiento. Un análisis de Pareto se enfoca en las categorías con mayores ventas para evaluar el movimiento de productos eficientemente, destacando la importancia de concentrar el análisis en productos clave para optimizar la toma de decisiones.
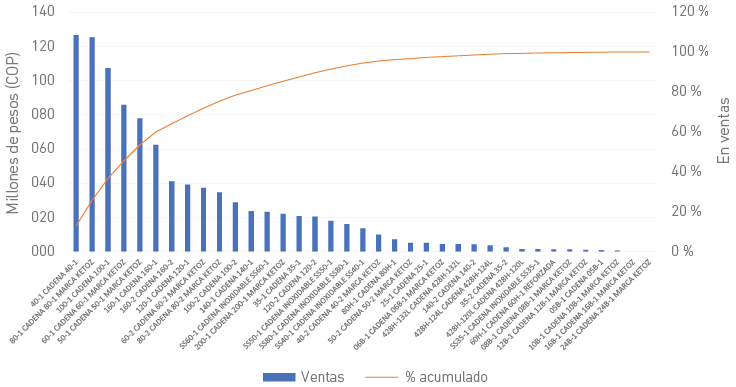
En la Figura 2, se presenta el análisis de Pareto que indica las cinco referencias más vendidas: cadenas 40-1, 80-1, 100-1, 60-1 y 160-1. Basándose en estas referencias, se desarrollarán tres escenarios que consideran los costos operativos, evaluando tanto la situación actual como escenarios hipotéticos con demanda estocástica y demanda determinística.
Figura 2
Pareto de ventas cadena de transmisión
Para el escenario determinístico, se evaluaron tres heurísticas: lote por lote, Silver-Meal y POQ. Se seleccionó finalmente la heurística POQ por su capacidad de ofrecer un periodo fijo que facilita la determinación de costos para todas las categorías, mientras que lote por lote y Silver-Meal se descartaron por su impracticabilidad y mayor frecuencia de pedidos, respectivamente, lo que incrementaría los costos (Nahmias, 2007). Se planea evaluar dos escenarios de tiempo de entrega: uno centrado en la categoría más vendida, la 40-1, y otro basado en el tiempo estándar de entrega para la mayoría de las categorías, manteniendo constantes los parámetros de costo y demanda del escenario actual y calculando el stock de seguridad (SS) a partir del promedio de demanda del periodo estudiado.
Durante la recopilación de datos, se analizaron registros históricos de ventas e inventarios para establecer la variabilidad en la demanda y los costos, asegurando la consistencia y confiabilidad de los datos con el sistema contable de la empresa. Se identificaron variables clave como costos, inventarios, niveles de servicio y cantidades de pedido. El tratamiento de los datos incluyó técnicas estadísticas para identificar patrones y tendencias. Los resultados se presentan en gráficos y tablas que resaltan las implicaciones para una gestión eficiente de inventarios. Este análisis apoya el diseño de una política de inventarios que minimiza costos y mejora la operatividad de la empresa. A continuación, se muestra la nomenclatura utilizada en este estudio.
Para determinar el costo de pedido kn para la referencia 40-1, se consideró el porcentaje de participación del producto con respecto al costo total de los productos, y se multiplicó por el valor de la importación. Este proceso se hace para cada una de las cuatro importaciones con el fin de obtener el costo de pedir para cada una de ellas. Los precios fueron los siguientes: $21 063 300,00, equivalentes al 8 % del valor total de la primera importación; $114 521 400,00, correspondientes al 33 % del valor total de la segunda importación; $13 740 860,00, que representan el 4,8 % del valor de la tercera importación. Posteriormente, se realizó la multiplicación del precio de pedido de cada importación por su porcentaje respectivo para obtener el k de cada importación.
Después de obtener los valores para cada kn, se procede a multiplicarlos por el porcentaje que abarca la importación n en el total de las unidades pedidas durante el periodo contemplado. Es decir, en la primera importación se pidieron 3050 unidades y el total de unidades pedidas en los 21 meses fue de 23 857; entonces, el peso de la importación 1 será el número de unidades pedidas en la importación sobre el total de unidades pedidas.
Obteniendo los pesos de cada una de las importaciones, se multiplicaron por el respectivo costo de pedir para cada importación.
Los costos de adquirir C para la referencia 40-1 en cada una de las importaciones se muestran a continuación:
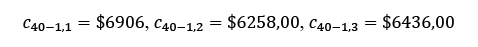
Con estos costos se realizó una suma producto entre los valores de adquirir y los pesos de la importación prn.
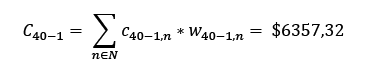
Para el cálculo del costo de inventario h, se asumió una tasa de mantener el inventario del 2 % mensual. Se obtuvo el siguiente costo de inventario por mes:
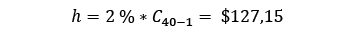
Para el cálculo de costos por faltantes, se realizó lo siguiente (pues es un costo unitario):
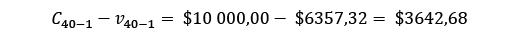
Después de analizar los datos, se observó que algunos periodos no registraron ventas debido a la falta de inventario en ciertas referencias. Para minimizar el impacto de estos faltantes en el análisis de la cantidad a pedir y los costos asociados, se decidió sustituir estos periodos sin ventas por el promedio de la demanda. Este ajuste permite un análisis más representativo al considerar la demanda potencial en los meses afectados por la escasez de inventario.
Para el escenario determinístico, se tuvo en cuenta la heurística POQ, que determinó una cantidad económica 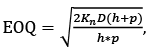donde D es igual al promedio de la demanda de los 21 meses contemplados. Para encontrar T dividimos la cantidad EOQ por la demanda,
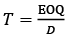(Nahmias, 2007). El costo por faltantes para cada categoría n se obtuvo calculando el número de periodos en los que no se vendió una unidad de dicha categoría, luego se dividió por el número total de periodos analizados para obtener el porcentaje en el que hubo faltantes. Posteriormente, se multiplica la demanda de cada mes por el porcentaje de faltantes y se multiplica por el costo de faltantes asociado a la categoría n.
Para la heurística Silver-Meal, en la cual se evalúa en qué periodo es más económico pedir la demanda de los siguientes hasta que se alcance la demanda esperada (Nahmias, 2007). Para el cálculo de pronósticos, se evalúa la tendencia que siguen las ventas de los 21 meses. Puede haber cuatro tipos de comportamiento: estacionario, con tendencia, con estacionalidad, y con tendencia y estacionalidad. Después de eso se determina el método de pronóstico por analizar.
Si la demanda tiene comportamiento estacionario, se utilizará la suavización exponencial simple, que inicializa el pronóstico con el promedio de los datos y continúa con el pronóstico del periodo: 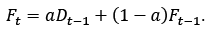Ya con el pronóstico de todos los meses, se encuentra el error:
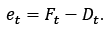Posteriormente, se halla el error medio:
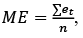y se minimiza el a, MIN a, donde 0,1 < a < 0,3, como muestra Nahmias (2007).
Una vez establecida la política de inventarios basada en el método teórico propuesto, comenzó la aplicación práctica integrando decisiones del modelo en los procesos operativos de la empresa, e implementando políticas de reorden y niveles de inventario óptimos. Durante esta fase, se monitorearon los niveles de inventario y costos, realizando un análisis comparativo con prácticas anteriores para evaluar la eficacia de la nueva política. Se observaron métricas como los niveles de inventario, costos operativos y eficiencia en la gestión de la demanda. Se identificaron desafíos y áreas de mejora, ajustando la política según fuese necesario. Las conclusiones del análisis destacaron que la nueva política mejoró la optimización de costos, la respuesta a la demanda variable y la mitigación de riesgos de importación. Se propusieron recomendaciones para futuros ajustes, promoviendo un enfoque dinámico y adaptable a cambios del mercado. Esta fase no solo marcó el fin del ciclo de implementación, sino que también sentó las bases para una mejora continua e innovación en la gestión de inventarios, alineada con los objetivos organizativos y las exigencias del entorno empresarial.
RESULTADOS
Evaluación del escenario actual
La Tabla 1 muestra los resultados de costos por categoría de producto para el escenario actual. La categoría 40-1 tiene el mayor costo de pedido debido a la alta cantidad de unidades solicitadas y al espacio que ocupa en el contenedor. Por ejemplo, en la importación de julio del 2022, la categoría 40-1 representó más del 60 % del espacio del contenedor. Las cadenas 160-1 y 100-1 presentan altos costos de adquisición por su gran tamaño, mientras que la 40-1 resulta ser la más económica gracias a la gran cantidad que se solicita a la fábrica.
Tabla 1
Costos por categoría de productos para el escenario actual
|
r = 40-1 |
r = 80-1 |
r = 100-1 |
r = 60-1 |
r = 50-1 |
r = 160-1 |
|
|
Kr |
$1 678 974,20 |
$1 291 010,19 |
$1 273 089,78 |
$847 573,75 |
$966 717,48 |
$730 483,41 |
|
Cr |
$6357,32 |
$25 296,67 |
$38 428,25 |
$14 196,03 |
$9 813,00 |
$94 464,00 |
|
hr |
$127,15 |
$505,93 |
$768,57 |
$283,92 |
$196,26 |
$1889,28 |
|
pr |
$3642,68 |
$14 703,33 |
$18 071,75 |
$8303,97 |
$5987,00 |
$43 036,00 |
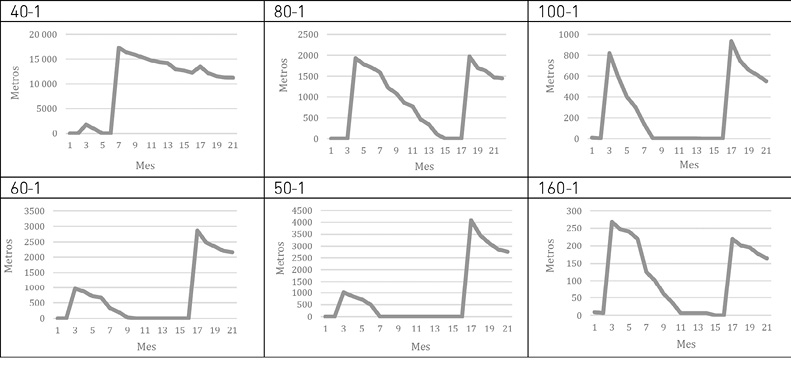
En la Figura 3 se observa la variabilidad en el inventario de la cadena 40-1: ausencias totales de stock durante cuatro meses y niveles bajo 5000 metros en los primeros seis meses. Aumentos significativos ocurren en los meses 3, 7 y 17, más notable en el mes 7, cuando el inventario supera los 15 000 metros. Si bien se incrementan los costos de mantenimiento, se reduce la necesidad de pedidos futuros. En contraste, la cadena 80-1 tiene un patrón más estable, con alrededor de 2000 metros, pero enfrenta tres meses de desabastecimiento antes de cada pedido, lo que afecta las ventas. La cadena 100-1 muestra 10 meses sin inventario, lo que indica pérdidas significativas en ventas. Las cadenas 60-1 y 50-1 reflejan variabilidad, con pedidos que aumentan considerablemente tras periodos sin stock, mientras que la cadena 160-1 tiene dos importantes recepciones de mercancía, aunque el último pedido fue menor pese a la escasez previa, desviándose de la política habitual de aumentar pedidos tras un desabastecimiento.
Figura 3
Inventarios por categoría de productos para el escenario actual
La Tabla 2 detalla los costos de operación para seis referencias de productos durante 21 meses, categorizados en costos de pedir, adquirir y mantener. La referencia 40-1 resulta ser la más costosa con un total de $183 208 118,51, principalmente por los altos costos de adquisición ($151 666 565,60) y mantenimiento ($26 504 630,31). La referencia 100-1 también presenta costos significativos, aunque menores, sumando $100 764 175,17. Las referencias 60-1 y 50-1 tienen costos totales de $90 620 287,17 y $78 781 707,11 respectivamente, influenciados principalmente por los costos de adquisición. Finalmente, la referencia 160-1 tiene el costo total más bajo de $65 555 074,21, pero con un costo de mantenimiento relativamente alto en comparación con su costo de adquisición. Estos datos subrayan la variabilidad de los costos asociados a cada referencia y la importancia de su consideración en la gestión de inventarios.
Tabla 2
Costos totales de operación en 21 meses para el escenario actual
|
Referencia |
40-1 |
80-1 |
100-1 |
|
Costo de pedir |
$5 036 922,60 |
$2 582 020,38 |
$2 546 179,56 |
|
Costo de adquirir |
$151 666 565,60 |
$115 732 250,00 |
$93 764 930,00 |
|
Costo de mantener |
$26 504 630,31 |
$11 244 165,96 |
$4 453 065,61 |
|
Costo total |
$183 208 118,51 |
$129 558 436,34 |
$100 764 175,17 |
|
Referencia |
60-1 |
50-1 |
160-1 |
|
Costo de pedir |
$1 695 147,50 |
$1 933 434,97 |
$1 460 966,82 |
|
Costo de adquirir |
$84 430 862,50 |
$74 824 125,00 |
$57 623 040,00 |
|
Costo de mantener |
$4 494 277,17 |
$2 024 147,14 |
$6 471 067,39 |
|
Costo total |
$90 620 287,17 |
$78 781 707,11 |
$65 555 074,21 |
Resultado para el escenario determinístico
Las heurísticas POQ y Silver-Meal fueron evaluadas utilizando la demanda actual para determinar cuál de ellas reduce más efectivamente los costos. La heurística POQ resultó ser más viable, ya que permite establecer un periodo de ciclo fijo, facilitando la evaluación de costos para las seis categorías analizadas bajo un mismo intervalo de tiempo (T). En cambio, la heurística Silver-Meal mostró una variabilidad significativa en los tiempos económicos de pedido para cada referencia, como se observa en la Figura 4 (los cuadros sombreados indican el periodo en que se pide), lo que llevó a su descarte. Finalmente, se decidió emplear la heurística POQ con periodos de ciclo fijos de seis y siete meses (T = 6 y T = 7) para simplificar y unificar el proceso de pedido.
Figura 4
Tiempos de pedido según la política Silver-Meal
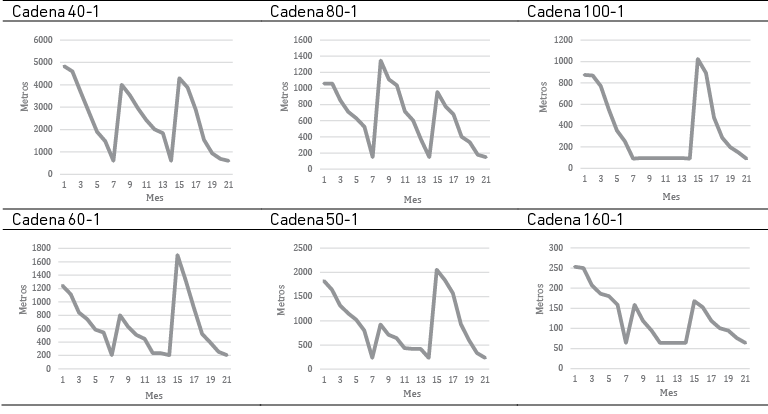
La Figura 5 muestra que el inventario de todas las referencias se mantiene sin agotarse completamente, gracias a la implementación de un stock de seguridad. Este método reduce el riesgo de desabastecimiento y cubre la demanda continua, aunque aumenta los costos de mantenimiento del inventario. En el análisis actual, se observa que más de tres referencias experimentaron agotamientos temporales, destacando el impacto económico de mantener un alto nivel de stock de seguridad. En cuanto a las cadenas 40-1, 60-1, 50-1 y 160-1, todas exhiben un patrón de inventario regular con un ciclo definido que alcanza el nivel de seguridad antes de hacer nuevos pedidos. Las cadenas 60-1 y 50-1, sin embargo, presentan variabilidad en las ventas que requiere ajustes en los pedidos. La cadena 100-1, aunque con un ciclo no definido y siete meses sin ventas, sigue un patrón similar.
Figura 5
Inventarios por categoría para un escenario determinístico
La Tabla 3 resume los costos totales de operación de seis referencias de producto durante 21 meses en un escenario determinístico, incluyendo costos de pedir, de adquirir, de mantener y por faltantes. La referencia 40-1 muestra un alto costo total de $95 970 183,67, principalmente por adquisición y mantenimiento, sin incurrir en costos por faltantes. En contraste, la 80-1 tiene el costo total más alto de $121 919 283,84, inflado por $4 802 415,40 en costos por faltantes. La 100-1 presenta el mayor costo por faltantes de $12 600 730,53, contribuyendo a un total de $86 027 161,18. Las referencias 60-1, 50-1 y 160-1 también registran costos totales considerables; sobresale la 160-1 por $4 434 854,92 en costos por faltantes.
Tabla 3
Costos totales de operación en 21 meses para un escenario determinístico
|
40-1 |
80-1 |
100-1 |
|
|
Costo de pedir |
$5 036 922,60 |
$3 873 030,57 |
$3 819 269,34 |
|
Costo de adquirir |
$84 312 221,14 |
$82 983 426,25 |
$76 414 026,15 |
|
Costo de mantener |
$6 621 039,94 |
$6 983 473,69 |
$5 793 865,68 |
|
Costo por faltantes |
$0 |
$4 802 415,40 |
$12 600 730,53 |
|
Costo total |
$95 970 183,67 |
$121 919 283,84 |
$86 027 161,18 |
|
60-1 |
50-1 |
160-1 |
|
|
Costo de pedir |
$2 542 721,25 |
$2 900 152,45 |
$2 191 450,23 |
|
Costo de adquirir |
$56 711 500,03 |
$50 092 865,02 |
$42 929 164,80 |
|
Costo de mantener |
$3 880 100,32 |
$3 810 603,79 |
$5 226 409,73 |
|
Costo por faltantes |
$1 579 687,07 |
$1 473 598,91 |
$4 434 854,92 |
|
Costo total |
$67 723 891,75 |
$60 969 186,46 |
$60 669 308,00 |
Pronósticos y aplicación de la política adecuada
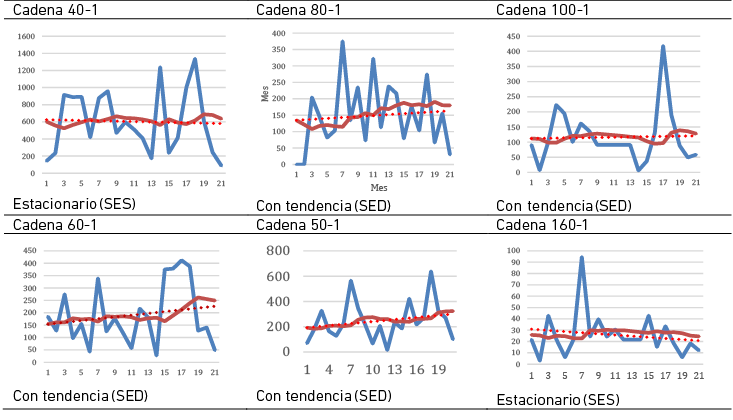
La Figura 6 compara la demanda real con los pronósticos para seis cadenas de productos utilizando modelos estacionarios (SES) y con tendencia (SED) a lo largo de 21 meses. En cadenas como la 40-1 y 160-1, donde se aplicó el modelo estacionario, los pronósticos se alinean razonablemente bien con la demanda plana, aunque no captan completamente los picos. Para las cadenas 80-1, 100-1, 60-1 y 50-1, modeladas con tendencia, los pronósticos siguen la tendencia general, pero fallan en prever picos abruptos y variaciones agudas, especialmente notable en la cadena 100-1 hacia el final del periodo.
Figura 6
Demanda vs. pronóstico
La Tabla 4 presenta los costos totales proyectados durante un periodo de 12 meses para seis referencias de producto. La referencia 80-1 registra el costo total más alto con $88 120 436,58, dominado por un elevado costo de adquisición de $76 799 770,42. En comparación, la referencia 100-1 también tiene costos significativos, que suman $60 069 111,41, con un costo de adquisición de $54 340 354,79. Las referencias 40-1 y 60-1 muestran costos totales de $43 091 670,44 y $44 122 102,96, respectivamente, cuyo costo de adquisición es el componente más grande para ambas. La referencia 50-1 cuenta con un costo total de $41 040 800,70, y la referencia 160-1 posee el costo total más bajo entre los productos analizados, con $21 921 292,82, lo que refleja costos más equilibrados entre pedir, adquirir y mantener.
Tabla 4
Costos totales a 12 meses para los datos pronosticados
|
40-1 |
80-1 |
100-1 |
|
|
Costo de pedir |
$1 678 974,20 |
$2 582 020,38 |
$3 819 269,34 |
|
Costo de adquirir |
$36 978 991,32 |
$76 799 770,42 |
$54 340 354,79 |
|
Costo de mantener |
$4 433 704,93 |
$8 738 645,78 |
$1 909 487,27 |
|
Costo total |
$43 091 670,44 |
$88 120 436,58 |
$60 069 111,41 |
|
Costo de pedir |
$2 542 721,25 |
$1 933 434,97 |
$1 460 966,82 |
|
Costo de adquirir |
$40 168 509,49 |
$37 057 644,05 |
$18 663 257,91 |
|
Costo de mantener |
$1 410 872,22 |
$2 049 721,68 |
$1 797 068,09 |
|
Costo total |
$44 122 102,96 |
$41 040 800,70 |
$21 921 292,82 |
Resultados del escenario estocástico
Para el escenario determinístico, se planteó el análisis utilizando los modelos Q, R y S, T; si bien ambos son factibles, el modelo que más se ajusta a la cadena de abastecimiento de la compañía es un modelo S, T, ya que define un periodo de tiempo fijo en el cual se debe realizar la orden y se calculará cuántas unidades de cada categoría faltan para alcanzar el nivel deseado de inventario. Para la realización de este método, se utilizan los mismos valores de k, c, h, p, del escenario actual, puesto que se van a considerar todos los escenarios con las mismas condiciones y datos históricos. Para la media μ, se tomó el promedio de los datos. Para la desviación σ, se tomó la desviación poblacional de los datos. Todos estos datos por referencia se pueden apreciar en la Tabla 5.
Tabla 5
Parámetros para el escenario estocástico por referencia
|
40-1 |
80-1 |
100-1 |
60-1 |
50-1 |
160-1 |
|
|
μ |
602,83 |
163,31 |
116,21 |
190,23 |
246,13 |
25,76 |
|
σ |
371,27 |
88,82 |
89,52 |
123,06 |
154,70265 |
19,22 |
|
a |
77 % |
76 % |
70 % |
76 % |
77 % |
69 % |
|
Q |
3990 |
912,94 |
620,48 |
1065,73 |
1557,162 |
141,15 |
|
T |
7 |
7 |
7 |
7 |
7 |
7 |
|
S |
8179,82 |
2036,93 |
2211,63 |
2584,8 |
3350,49 |
342,67 |
|
SS |
945,87 |
251,91 |
164,67 |
302,01 |
396,89 |
33,52 |
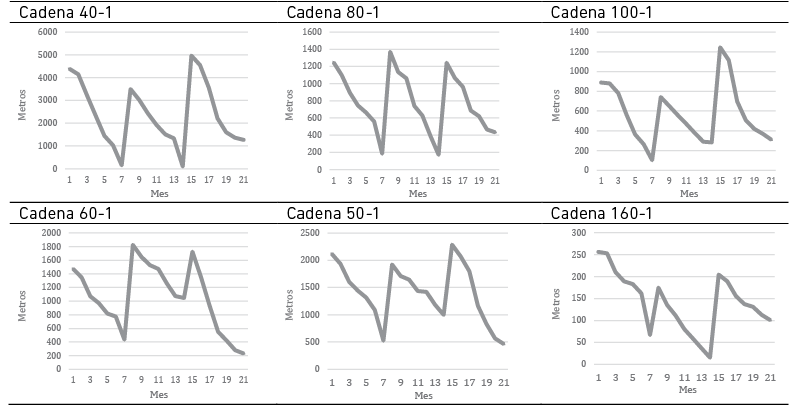
La Figura 7 muestra los inventarios de seis categorías de productos bajo un escenario estocástico a lo largo de 21 meses. Cada gráfico revela fluctuaciones notables en los niveles de inventario. La cadena 40-1 experimenta oscilaciones significativas, alcanzando picos y valles pronunciados. De manera similar, las cadenas 80-1 y 100-1 exhiben patrones de alza y baja con cierta regularidad. Las cadenas 60-1 y 50-1 también reflejan variabilidad en sus inventarios, con subidas y bajadas en el tiempo, aunque la cadena 50-1 presenta un pico particularmente alto hacia la mitad del periodo observado. Por último, la cadena 160-1, aunque con menos amplitud en las fluctuaciones, sigue un patrón de picos y caídas.
Figura 7
Inventarios por categoría para el escenario estocástico
La Tabla 5 presenta los costos totales de operación para seis categorías de productos durante un periodo de 21 meses en un escenario estocástico, desglosando los costos en ordenar, adquirir, mantener y faltantes. En todas las categorías, el costo de adquirir domina el gasto total. Para la referencia 40-1, los costos ascienden a $95 259 517 con un notable monto asignado a faltantes de $90 013,55. La 80-1 y 100-1 tienen costos totales de $93 465 120,48 y $109 989 738,79 respectivamente, pero también muestran cifras significativas en faltantes. Las referencias 60-1, 50-1 y 160-1 tienen costos totales de $66 520 560,27, $60 090 978,46 y $59 895 803,09 respectivamente, entre las cuales la 160-1 presenta el menor costo en faltantes con $80 514,93.
Tabla 5
Costos totales de operación para 21 meses para el escenario estocástico
|
40-1 |
80-1 |
100-1 |
|
|
Ordenar |
$239 853 |
$184 430 |
$181 870 |
|
Adquirir |
$3 832 374 |
$3 771 974 |
$4 465 755 |
|
Mantener |
$373 927 |
$389 314 |
$439 162 |
|
Faltantes |
$90 013 55 |
$105 001,75 |
$150 820,35 |
|
Total (mes) |
$4 536 168 |
$4 450 720 |
$5 237 607 |
|
Total (periodo) |
$95 259 517 |
$93 465 120,48 |
$109 989 738,79 |
|
Ordenar |
$121 082 |
$138 102 |
$104 355 |
|
Adquirir |
$2 700 548 |
$2 415 304 |
$2 433 626 |
|
Mantener |
$274 785 |
$246 966 |
$233 685 |
|
Faltantes |
$71 230,79 |
$61 102,97 |
$80 514 93 |
|
Total (mes) |
$3 167 646 |
$2 861 475 |
$2 852 181 |
|
Total (periodo) |
$66 520 560,27 |
$60 090 978,46 |
$59 895 803,99 |
Comparación de costos
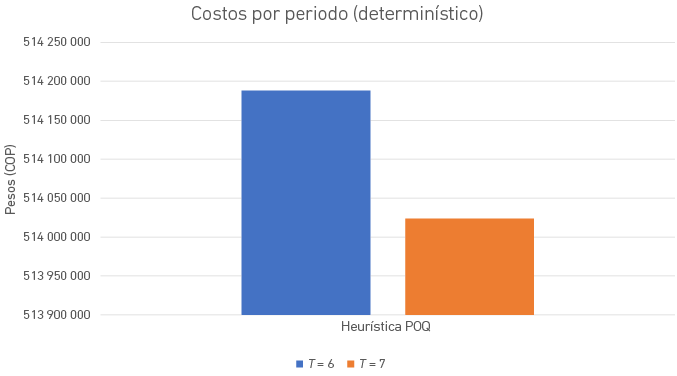
En la comparación de las dos mejores instancias para el método determinístico, que se expone en la Figura 8, se evaluaron los periodos T = 6 y T = 7. Al analizar los costos, se encontró que realizar pedidos cada siete meses permite a la empresa ahorrar $ 164 256,65. Aunque este ahorro no es considerablemente alto, contribuye a la reducción de costos operativos. Por lo tanto, se decidió adoptar un ciclo de pedido de cada siete meses (T = 7) como la estrategia más costo-efectiva.
Figura 8
Comparación de costos por periodo para escenario determinístico
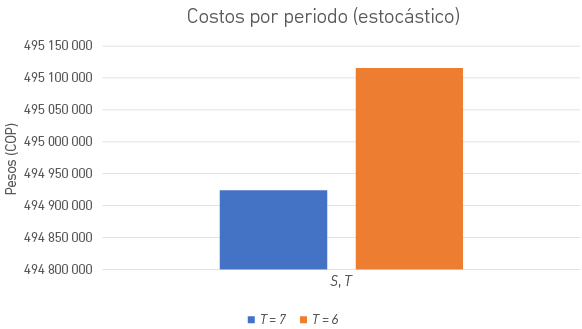
La Figura 9 muestra una comparación de los costos operativos para dos periodos de revisión del inventario bajo un escenario estocástico, específicamente con ciclos de pedido T = 7 y T = 6. En el gráfico, se observa que el costo total para el ciclo T = 7 es aproximadamente $493 700 000, mientras que para el ciclo T = 6 es cercano a $494 300 000, lo que evidencia un ahorro al optar por un ciclo de pedido más largo (T = 7). Aunque la reducción no es significativamente grande, representa una disminución en los costos operativos en comparación con el ciclo más corto (T = 6).
Figura 9
Tabla de comparación de costos por periodo para escenario estocástico
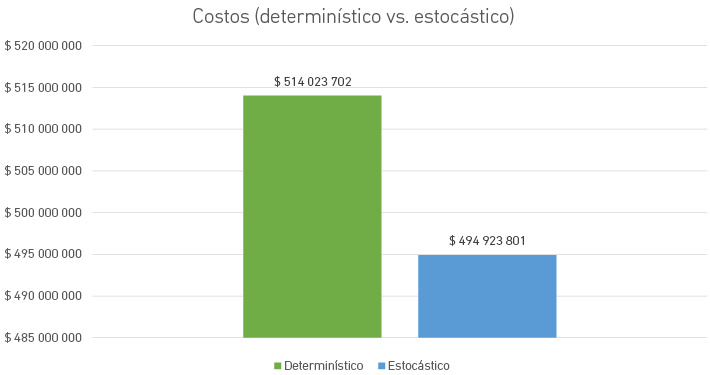
La Figura 10 ilustra una comparación de los costos totales asociados con dos enfoques de gestión de inventario: determinístico y estocástico. Según el gráfico, el enfoque determinístico incurre en un costo considerablemente más alto, que asciende a $514 023 701,52, en comparación con el enfoque estocástico, que presenta un costo de $493 665 514,31. Esto sugiere que, en este caso, el enfoque estocástico es más eficiente desde el punto de vista de costos, ahorrando aproximadamente $20 358 187,21, lo que indica una ventaja económica en optar por métodos que consideren la variabilidad y la incertidumbre inherentes en la gestión del inventario.
Figura 10
Diagrama de costos por cada alternativa
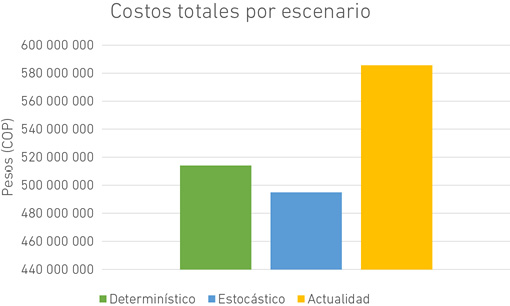
La Figura 11 muestra los costos totales asociados con tres diferentes escenarios de gestión de inventario: determinístico, estocástico y la situación actual de la empresa. Según el gráfico, el escenario actual es el más costoso, con un gasto total cercano a $580 000 000. En contraste, el escenario determinístico presenta costos significativamente más bajos, aproximadamente $500 000 000, mientras que el escenario estocástico presenta el costo más reducido de los tres, alrededor de $480 000 000. Este análisis sugiere que tanto los enfoques determinístico como estocástico de gestión de inventario resultan en ahorros considerables en comparación con el enfoque actual, pero destaca especialmente la eficiencia del modelo estocástico en términos de costos.
Figura 11
Diagrama de costos por cada alternativa
DISCUSIÓN
La implementación efectiva de modelos determinísticos y estocásticos en la gestión de inventarios ha mostrado un impacto significativo en la reducción de periodos sin inventario, en contraste con el escenario actual, que presenta riesgos de desabastecimiento considerable. Según investigaciones de Bai y Zhong (2008), la elección del modelo de inventario adecuado puede variar ampliamente dependiendo de las condiciones del mercado y la variabilidad de los proveedores, lo que resalta la necesidad de un enfoque adaptable y sensible a contextos internacionales. Tanto el modelo determinístico, con opciones de T = 6 y T = 7, como el estocástico (método S, T) han optimizado la gestión de inventarios, como sostienen Parga-Prieto y Aranda-Pinilla (2018) al destacar la utilidad de técnicas heurísticas avanzadas para ajustar los periodos de pedido en función de las demandas del mercado.
Además, la introducción de un inventario de seguridad en ambos modelos representa un cambio estratégico crucial en la gestión de inventarios, siguiendo las sugerencias de González (2020) sobre la importancia de utilizar coeficientes de variación y suavización exponencial para responder a cambios en la demanda. Este enfoque es especialmente relevante en industrias como la textil y la de productos perecederos, donde, según Triana (2022) y Rodríguez y Vidal (2009), es crítico adaptar los métodos de pedido para gestionar eficazmente las peculiaridades de la demanda estacional y los ciclos de vida cortos. El inventario de seguridad ha probado ser esencial para mitigar riesgos y asegurar una operatividad continua, reflejando la innovación y mejora continua en los procesos de inventario, como mencionan Rojas Mancipe (2011) y Silva Gómez (2017).
Estos ajustes estratégicos no solo fortalecerán la estabilidad operativa de la empresa, sino que también reducirán significativamente los costos asociados con la escasez de inventario. Esto demuestra la importancia de adaptar estrategias de inventario para enfrentar efectivamente la variabilidad en la demanda y los desafíos en la cadena de suministro.
CONCLUSIONES
La implementación del método determinístico mediante la heurística POQ ha demostrado que un tiempo de ciclo de siete meses optimiza los costos de gestión de inventarios y aumenta la robustez del sistema frente a fluctuaciones de demanda. Este método ha mejorado notablemente la eficiencia en la gestión de inventarios, aunque es vital continuar monitoreando y adaptando las estrategias debido a la variabilidad de la demanda. En contraste, el escenario actual carece de un ciclo definido, lo que ha llevado a frecuentes faltantes y excesos de inventario, lo que indica desequilibrios entre la oferta y la demanda, y genera costos adicionales.
Por otro lado, el método estocástico, específicamente el modelo (S, T), ha resultado ser más rentable en comparación con el escenario actual y el determinístico, principalmente por la reducción de faltantes y la homogeneidad en el comportamiento del inventario. La adopción de un ciclo de pedidos cada siete meses ha equilibrado efectivamente la oferta y la demanda, facilitando una gestión más coherente y previniendo escasez o excesos. Este modelo estocástico se adapta mejor a la variabilidad y la incertidumbre del mercado, permitiendo a la empresa responder de manera más efectiva a los cambios del entorno.
En conclusión, la transición al modelo estocástico (S, T) y la frecuencia de pedidos cada siete meses mejorarían significativamente la gestión de inventarios. La implementación de un stock de seguridad y la elección adecuada de estrategias, como la heurística POQ, contribuirían a una cadena de suministro más eficiente y adaptable. Dada la variabilidad inherente en la demanda del mercado, se recomienda utilizar modelos estocásticos que consideren la incertidumbre y permitan una planificación más flexible y dinámica, en contraste con los modelos determinísticos, que asumen una demanda constante y predecible.
DECLARACIÓN DE CONFLICTOS DE INTERÉS
Para la investigación titulada “Gestión de inventarios de una compañía importadora de repuestos de transmisión de potencia de maquinaria pesada”, los autores declaran que no existen conflictos de intereses financieros, personales o profesionales que puedan influir en los resultados del estudio. Ninguno de los autores ha recibido financiamiento o mantiene relaciones que puedan afectar la objetividad e integridad de esta investigación.
DECLARACIÓN DE CONTRIBUCIÓN A LA AUTORÍA
Mateo Núñez-Oviedo: conceptualización, data curation, análisis formal, investigación, metodología, administración de proyecto, recursos, software, visualización, escritura: borrador-original, redacción: revisión y edición. Luis Tarazona-Torres: conceptualización, metodología, supervisión, validación, redacción: revisión y edición.
REFERENCIAS
Alves, P., Delgado, K., Freire, A., & Silva, V. (2017). Sistema para resolver o problema de roteamento e inventário com demanda estocástica: comparando diferentes heurísticas na relaxação lagrangeana. En J. M. David & A. Pimienta (Coords.), 2017: Actas del XIII Simposio Brasileño de Sistemas de Información (pp. 555-562). https://doi.org/10.5753/sbsi.2017.6087
Arango, M. D., Adarme-Jaimes, W., & Otorno, M. A. (2011). Coordinación de abastecimiento con información compartida en pymes agroalimentarias colombianas. DYNA, 78(167), 203-212. https://repositorio.unal.edu.co/handle/unal/8748
Ardila, J. A. (2010). Selección de un modelo de coordinación de inventarios para la bodega y farmacias auxiliares de un hospital público en Bogotá [Tesis de maestría, Universidad de los Andes]. Repositorio Institucional Séneca de la Universidad de los Andes. http://hdl.handle.net/1992/11490
Bai, L., & Zhong, Y. (2008). Improving inventory management in small business: A case study [Tesis de maestría, Universidad de Jönköping]. Repositorio Institucional de la Universidad de Jönköping. https://urn.kb.se/resolve?urn=urn%3Anbn%3Ase%3Ahj%3Adiva-1136
Ballou, R. H. (2004). Logística. Administración de la cadena de suministro. Pearson Educación.
Baron, O., Berman, O., & Perry, D. (2017). Continuous review inventory models for perishable items with leadtimes. Probability in the Engineering and Informational Sciences, 34(3), 317-342. https://doi.org/10.1017/S0269964817000225
Carvajal, J., & Amaya, C. (2011). Un enfoque mate-heurístico para solucionar el problema de distribución e inventario con múltiples productos, múltiples minoristas y un solo centro de distribución con restricciones de presupuesto, un caso de estudio: sistema de abastecimiento de medicamentos en una caja de compensación familiar, seccional salud [Tesis de maestría, Universidad de los Andes]. Repositorio Institucional Séneca de la Universidad de los Andes. http://hdl.handle.net/1992/11360
Chopra, S., & Meindl, P. (2008). Administración de la cadena de suministro. Estrategia, planeación y operación (3.a ed.). Pearson Educación.
Contreras Juárez, A., Atziry Zúñiga, C., Martínez Flores, J. L., & Sánchez Partida, D. (٢٠١٨). Gestión de políticas de inventario en el almacenamiento de materiales de acero para la construcción. Revista Ingeniería Industrial, 17(1), 5-22. https://doi.org/10.22320/S07179103/2018.01
Gonçalves, J. N. C., Carvalho, M. S., & Cortez, P. (2020). Operations research models and methods for safety stock determination: A review. Operations Research Perspectives, 7, 100164 http://dx.doi.org/10.1016/j.orp.2020.100164
González, A. (2020). Un modelo de gestión de inventarios basado en estrategia competitiva. Ingeniare. Revista Chilena de Ingeniería, 28(1), 133-142. http://dx.doi.org/10.4067/S0718-33052020000100133
Guzmán-Camacho, C. H., Salazar-Sanabria, H., & Adarme-Jaimes, W. (2014). Coordinación de inventarios en la recolección de leche cruda. Caso región Sugamuxi-Colombia. DYNA, 81(186), 259-266. https://doi.org/10.15446/dyna.v81n186.45216
Martínez Arteaga, M. F. (2016). Diagnóstico del control de inventarios en las panaderías de tipo microempresa de la ciudad de Pasto (Colombia) y modelo matemático para la gestión de inventarios [Tesis de maestría, Universidad de los Andes]. Repositorio Institucional Séneca de la Universidad de los Andes. http://hdl.handle.net/1992/13938
Monisola, O. (2013). An assessment of inventory management in small and medium scale industrial enterprises in Nigeria. European Journal of Business and Management, 5(28), 150-158. https://www.iiste.org/Journals/index.php/EJBM/article/view/8727
Nahmias, S. (2007). Análisis de la producción y las operaciones (5.a ed.). McGraw Hill.
Parga-Prieto, A. T., & Aranda-Pinilla, J. A. (2018). Políticas de inventario para demandas con tendencia y aleatoriedad. Caso comercializadora de lubricantes. Inventum, 13(24), 50-57. https://doi.org/10.26620/uniminuto.inventum.13.24.2018.50-57
Pérez Hualtibamba, M. M., & Wong Aitken, H. G. (2018). Gestión de inventarios en la empresa SOHO Color Salón & Spa en Trujillo (Perú), en 2018. Cuadernos Latinoamericanos de Administración, 14(27). https://doi.org/10.18270/cuaderlam.v14i27.2457
Rangel Vega, L. (2016). Definir el modelo de gestión de inventarios para múltiples productos, dentro del procedimiento de compras en Civalco Ltda. [Tesis de maestría, Universidad de los Andes]. Repositorio Institucional Séneca de la Universidad de los Andes. http://hdl.handle.net/1992/13789
Restrepo, M. C., Chamorro, C., & Carvajal, D. (2020). El control interno de los inventarios: su incidencia en la gestión financiera de “Due Amici Pizzería”. Revista Activos, 18(2), 137-163. https://doi.org/10.15332/25005278/6264
Rodríguez, J. A., & Vidal, C. J. (2009). A heuristic method for the inventory control of short life-cycle products. Ingeniería y Competitividad, 11(1), 37-55. http://www.redalyc.org/articulo.oa?id=291323535004
Rojas Mancipe, A. (2011). Simulación de una cadena de abastecimiento productor-comprador con un mecanismo de coordinación de inventarios según el modelo VMI con demanda estocástica [Tesis de grado, Universidad de los Andes]. Repositorio Institucional Séneca de la Universidad de los Andes. http://hdl.handle.net/1992/14742
Silva Gómez, J. (2017). Programación de pedidos y optimización de la cadena de suministro de Black Jack Importaciones SAS [Tesis de grado, Universidad de los Andes]. Repositorio Institucional Séneca de la Universidad de los Andes. http://hdl.handle.net/1992/61863
Triana, I. D. (2022). Modelo de inventarios bajo demandas estacionales [Tesis de maestría, Universidad de los Andes]. Repositorio Institucional Séneca de la Universidad de los Andes. http://hdl.handle.net/1992/57461
Wiśniewski, J. W. (2021). Forecasting in small business management. Risks, 9(4), 69. https://doi.org/10.3390/risks9040069