D-01_2_INGENIERIA

Optimización de parámetros
con enjambre de partículas
en un molde de colada continua*

Yordy González Rondón

https://orcid.org/0000-0002-4769-7568

Universidad de Oriente, Instituto de Investigaciones en Biomedicina y Ciencias Aplicadas, IIBCAUDO “Dra. Susan Tai”, Cumaná, Estado Sucre, Venezuela.

Universidad de Oriente, Núcleo de Anzoátegui, Departamento de Mecánica,
Barcelona, Estado Anzoátegui, Venezuela

José Eduardo Rengel Hernández

https://orcid.org/0000-0002-4510-8846

Universidad de Oriente, Núcleo de Anzoátegui, Departamento de Mecánica,
Barcelona, Estado Anzoátegui, Venezuela

Johnny Martínez Rizales

https://orcid.org/0000-0001-8901-9303

Universidad de Oriente, Núcleo de Anzoátegui, Departamento de Mecánica,
Barcelona, Estado Anzoátegui, Venezuela

Recibido: 22 de febrero del 2021 / Aprobado: 11 de mayo del 2021

doi: https://doi.org/10.26439/ing.ind2021.n41.5100

RESUMEN: Con la finalidad de ajustar en el molde de colada continua los parámetros que influyen en la aparición de defectos en el acero, se ha desarrollado un algoritmo de optimización por enjambre de partículas (PSO), haciendo uso de modelos de procesos. El estudio consideró múltiples objetivos con múltiples restricciones y los resultados fueron comparados con los reportados por un algoritmo de optimización basado en enseñanza-aprendizaje (TLBO). Se concluyó que el PSO tiene buena capacidad para determinar los parámetros del molde y, con él, es posible conseguir una solución óptima sin requerir grandes esfuerzos computacionales.

PALABRAS CLAVES: optimización de parámetros / colada continua / enjambre de partículas, metaheurísticas / molde de colada

Parameter Optimization with Particle Swarm
in a Continuous Cast Mold

ABSTRACT: To adjust the parameters that influence the appearance of defects in the steel in the continuous casting mold, a particle swarm optimization algorithm (PSO) was developed using process models. The study considered multiple objectives with multiple restrictions and the results were compared with those reported by a teaching-learning-based optimization algorithm (TLBO). We conclude that the PSO has a good capacity to determine the parameters of the mold, and with it, it is possible to achieve an optimal solution without requiring great computational efforts.

KEYWORDS: parameter optimization / continuous casting / particle swarm / metaheuristics
/ casting mold.

** Todos autores han contribuido con la misma intensidad en el diseño, obtención de datos, analisis, revisión crítica de su contenido y aprobación final de la versión publicada.

1. INTRODUCCIÓN

El primer paso para lograr la transformación masiva del arrabio en acero lo dio el inglés Henry Bessemer en 1855 (Calvo, 2006; Mannheim, 1983; Najera, 2010). Mucho más tarde en Europa, en los años cincuenta del siglo xx, en un intento por incrementar la producción de acero se desarrolló el proceso de colada continua (PCC) (Flores, 2010). Se denominó continua porque permite la solidificación del metal líquido en un tiempo muy corto y el retiro inmediato del molde (Coley, 2010; Kumar, 2015). La ventaja más importante del proceso es la regularidad (Aballe, 1992), pues con ella se ha conseguido, en las últimas décadas, grandes avances en la producción (Cruz et al., 2007; Hahn et al., 2012), al igual que su consumo (Saldaña et al., 2019).

Figura 1. Proceso de la colada continua del acero (PCC)

Elaboración propia

En la figura 1 se muestra el PCC; este se inicia cuando la cuchara recibe acero líquido proveniente del horno de arco eléctrico o bien del convertidor (Romo, 2009); allí se almacena y luego se introduce en una artesa con la finalidad de ser homogenizado (Calvo, 2006). Posteriormente se deja fluir a través de una boquilla de entrada sumergida (BES) hacia un molde de cobre de alta pureza, de 10 a 20 mm de espesor (Kumar, 1996), con longitud de 500 a 800 mm (Romo, 2009), sin fondo y enfriado por agua (Belisario, 2011; Romo, 2009). El acero líquido se solidifica por el contacto con las paredes del molde refrigerado, formando una costra que durante su evolución se contrae y forma separaciones intermitentes con las paredes (Najera, 2010). Para evitar que la costra se adhiera al molde se utilizan movimientos oscilatorios y para disminuir la fricción se agregan polvos de fundición por la parte superior del molde, que con el avance del fundido se infiltra entre el molde y la costra de acero solidificado (Kumar, 1996; Romo, 2009). El polvo, durante su descenso, forma una película de escoria líquida y una capa de escoria sólida de 0,1 mm y 2 mm de espesor, respectivamente. Estos espesores interfieren en el flujo de calor extraído por el molde (Cicutti, 1977; Mills et al., 2014). El proceso continúa con la salida de la pieza por la parte inferior del molde, alcanzando un espesor de 12 a 25 mm, lo suficientemente fuerte para evitar desgarros y roturas debido a la presión ferrostática (Chang y Bolsaitis, 1982; Cruz et al., 2007). La pieza se enfriará en la zona de enfriamiento secundario con agua pulverizada y aire. El PCC finaliza cuando el producto es cortado por medio de sistema oxicorte en planchones, palanquillas o tochos (Chang y Bolsaitis, 1982; Cicutti, 1977; Kumar, 2015; Najera, 2010).

El objetivo principal del PCC es extraerle calor al acero líquido en un tiempo muy corto (Cicutti, 1977; Najera, 2010), y de todos los elementos que lo conforman, el molde es el más importante (Najera, 2010; Romo, 2009), porque allí debe lograrse (a) un ajuste adecuado de los parámetros que definen la formación de una costra solidificada con características específicas y (b) condiciones adecuadas en los fenómenos de transferencia de calor y flujo de fluidos (Adilson et al., 2018; Zhang et al., 2017), por el impacto en el origen de defectos en el acero como marcas, segregación, grietas, inclusiones, entre otros (Adilson et al., 2018; Hahn et al., 2012). Estos defectos influyen en las propiedades mecánicas del acero y, para disminuirlos, se deben ajustar los parámetros operacionales (Aballe, 1992; Hahn et al., 2012) y vencer las principales dificultades que son: adptar una velocidad de colada a la velocidad de solidificación y establecer las condiciones de enfriamiento y lubricación en el molde (Najera, 2010).

Concast Data Sheets (1992), basado en literaturas y datos de la industria, describió que los defectos en la colada continua se deben en un 16 % a prácticas de fundición defectuosas, el 29 % a las malas condiciones de la máquina, el 38 % al mal ajuste en los valores de los parámetros del proceso, y el 17 % a la composición química del acero. Estos resultados demuestran que para obtener productos de acero con buena calidad (mínimos defectos) es necesario conseguir los mejores ajustes en los parámetros que intervienen en el molde. Es común que en las plantas de fundición se utilice el método de prueba y error para determinar los parámetros, pero este procedimiento requiere de la inversión de largos periodos de trabajo experimental, que traen como consecuencia pérdidas de tiempo y dinero (Venkata et al., 2014). Por lo antes expuesto, en esta investigación se plantea el uso de una metaheurística de optimización para ajustar los parámetros de la zona del molde, entre las más conocidas se tiene (a) la optimización por enjambre de partículas “PSO” (Kennedy y Eberhart, 1995; Kennedy et al., 2001), perteneciente a la familia de los algoritmos bioinspirados (Bäck, et al., 1997; Stephan y Zomaya, 2005), (b) los algoritmos evolutivos (Bäck et al. 1997), (c) las colonias de hormigas (Dorigo, 2000), y (d) la optimización basada en enseñanza-aprendizaje (Rao, et al. 2011; 2012; Rao y Patel, 2012). En la búsqueda de antecedentes sobre la aplicación de estas técnicas en el proceso de colada continua, se tiene a Yu y Luo (2017) quienes presentaron un algoritmo de evolución diferencial para estimar los coeficientes de transferencia de calor en una palanquilla de acero. Wang et al. (2019) presentaron un método de solución en paralelo de dos niveles para identificar los coeficientes de transferencia de calor usando el PSO. Wang, et al. (2016) presentaron un método para predecir el comportamiento de transferencia de calor en el enfriamiento secundario, haciendo uso del PSO. Wang et al. (2020) propusieron un algoritmo de optimización mejorado mediante enjambre de partículas para la distribución del agua de enfriamiento en la zona secundaria. Li y Zang (2021) diseñaron un algoritmo de optimización inteligente que combinó PSO y red neuronal para establecer un modelo de predicción de defectos comunes en la colada continua. Luo et al. (2017), presentaron un enfoque que integró la función Gaussian Kernel (GK) y el PSO para la estimación de los coeficientes de transferencia de calor en el PCC. Feng et al. (2020), optimizaron los parámetros de un controlador difuso mediante el uso de un algoritmo PSO. García Nieto et al. (2018), presentaron un novedoso algoritmo híbrido, que combinó la técnica PSO para predecir la segregación en losas de acero mediante colada continua. Venkata et al. (2014), demostraron la aplicabilidad del TLBO en el ajuste de parámetros en el molde de colada continua de acero e hicieron referencia al método de optimización por recocido simulado (SA). Es de notar que en la zona de enfriamiento secundario del proceso de colada continua de acero se ha estudiado la optimización de parámetros, pero en la zona del molde no se ha prestado suficiente atención; además, no se ha encontrado gran aplicabilidad de la técnica de enjambre de partículas PSO sobre el ajuste de los parámetros del molde, que pudieran minimizar la aparición de ciertos defectos en el acero. En este sentido, la presente investigación plantea el desarrollo de un algoritmo PSO en Fortran 90, para determinar los valores adecuados de ciertos parámetros en el molde del PCC, que guardan relación con la aparición de algunos defectos. En el procedimiento se consideran los criterios descritos por Kulkarni y Subash Babu (2001, 2003, 2005; Venkata et al. (2014), y se espera que con los resultados se valide la aplicabilidad y eficiencia del PSO en el molde de colada.

2. MATERIALES Y MÉTODOS

El presente artículo trata de una investigación aplicada, que tiene como propósito encontrar estrategias, a partir de conocimientos teóricos, para generar conocimiento práctico. En este sentido se hace una descripción de los pasos que se han aplicado para la optimización de los parámetros del molde de colada continua, empleando el método de enjambre de partículas.

2.1 Condiciones del molde para una fundición sin defectos

Conocer los modelos que involucran las variables del molde de colada continua es fundamental para determinar el ajuste en los parámetros del proceso. Kulkarni y Babu (2001) desarrollaron un sistema integrado que consta de metamodelos, que resultó ser útil, preciso y al mismo tiempo muy eficiente, ya que requería tratar pocas ecuaciones. Kulkarni y Babu (2003) desarrollaron un sistema integrado que consta de modelos de proceso; este sistema resultó ser importante para comprender y analizar el sistema de colada continua. Kulkarni y Babu (2005) presentaron una serie de características relacionadas con la calidad, así como algunas condiciones del proceso relacionadas con las características y parámetros relacionados con la condición de qué influyen en los defectos. Con base en estos estudios, en este trabajo se han identificado diez condiciones principales que relacionan los parámetros del molde, tal como se describen en la tabla 1. Es importante resaltar que las condiciones descritas en la tabla 1 deben cumplir con las restricciones, porque de no ser así, la probabilidad de aparición de defectos en el acero aumentará, razón por la que en este trabajo se busca satisfacer todas las restricciones.

2.2 Función de pérdida en las condiciones del molde

Luego de seleccionar las expresiones involucradas en el molde, es necesario adoptar funciones de pérdida en cada una de las condiciones de la tabla 1. Para éstos es importante que cada expresión involucre una medida de indeseabilidad para cuantificar el cumplimiento de la condición. La función de pérdida correspondiente a la condición, tomará el valor de uno (1) si las magnitudes de los parámetros involucrados en las expresiones hacen que el valor de la restricción se acerque a los extremos. Y la indeseabilidad total será la suma de las indeseabilidades individuales. Bajo este método, la calidad del producto se verá afectada cuando no se cumplan las condiciones.

Tabla 1
Condiciones para una fundición sin defectos

Nota: Donde, ŋes la viscosidad de equilibrio en poise, Vc es la velocidad de fundición en m/min., Tsol es la temperatura de solidificación del flujo del molde en °C, s es la longitud de carrera en mm, f la frecuencia en ciclos por minutos cpm, Vm es la velocidad del molde en m/min, Rp es la velocidad de drenaje en m/min, p es la densidad del flujo líquido de lubricante en kg/m3, Tsurf es la temperatura de la superficie de la costra en °C, Lm es la longitud del molde en m, K es una constante (K = 0,251), y la dimensión de la cara ancha en m.

Fuente: Kulkarni y Babu (2001, 2003, 2005), Venkata et. al (2014)

Tabla 2
Funciones de pérdida para los criterios de calidad

Fuente: Kulkarni y Babu (2001, 2003, 2005), Venkata et. al (2014)

La llamada función de pérdida deriva de la teoría de Taguchi (Hernández, 1994), que establece una función de pérdida parabólica con vértice en el valor nominal (valor deseado). Según la teoría, la pérdida empieza a darse cuando los resultados comienzan a separarse del valor deseado (m); además, crece de forma cuadrática como corresponde a una parábola. La teoría pretende penalizar la mayor desviación del valor nominal, y la ecuación de la parábola donde “nominal es mejor” según la siguiente expresión (Hernández, 1994):

(1)

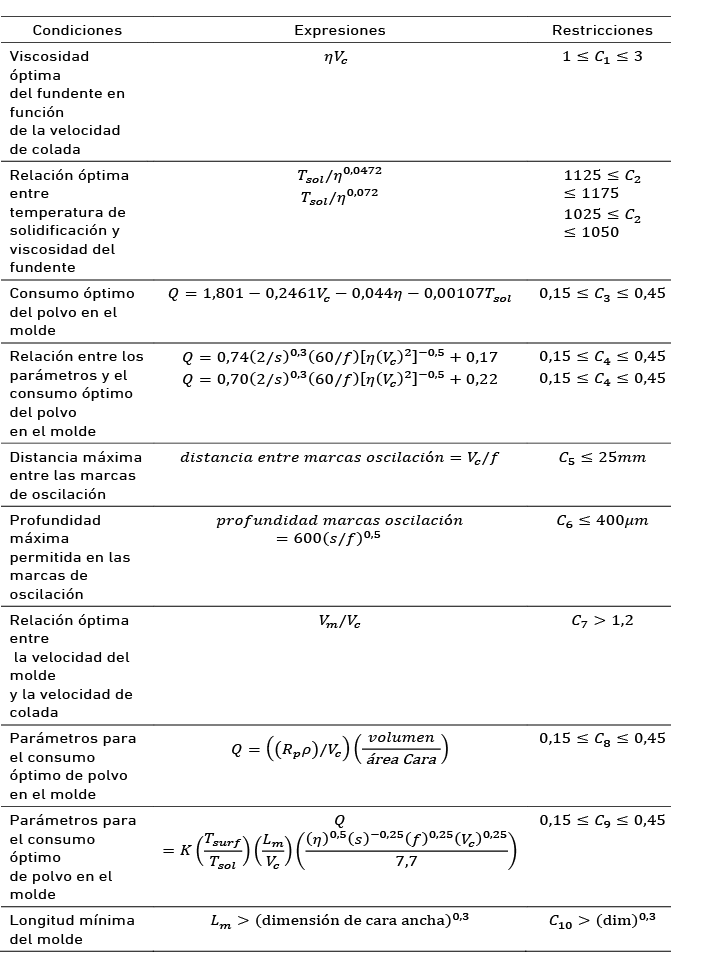
Donde P es la pérdida, x es la característica de calidad medida, m es el rendimiento objetivo, y k es el coeficiente de pérdida. En ciertas restricciones de la tabla 1 se presentan situaciones en las que, cuanto mayor sea el valor de la característica de calidad, mejor sería el beneficio, o cuanto menor sea el valor de la característica de calidad, mejor sería el beneficio. En tales casos, se utilizan diferentes formas de función de pérdida. Para cuando “menor es mejor” (Hernández, 1994):

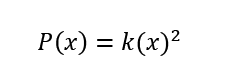(2)

Y para cuando “mayor es mejor” (Hernández, 1994):

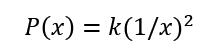(3)

Basados en (1), (2) y (3) se establecieron las funciones de pérdida en cada una de las condiciones críticas; los resultados se muestran en la tabla 2. Como las respuestas están en diferentes unidades, se hacen conversiones a una misma escala usando el coeficiente de pérdida “k”, de tal manera que, para el límite mínimo o máximo en la restricción, el valor de pérdida individual se convierte en 1, y será 0 para el valor que se haya aceptado como característica de calidad.

2.3 Identificación de la función objetivo

Como se están considerando varias condiciones, la indeseabilidad total será la suma de los valores de índice individuales, según:

(4)

El valor ideal para la función de pérdida total PT es cero (0) y el peor escenario será diez (10). Con este procedimiento se tendrá como objetivo de optimización encontrar las posibles combinaciones en las magnitudes de los parámetros del molde que minimicen la función de pérdida total, satisfaciendo cada una de las restricciones, porque cuanto mayor sea el valor de la función de pérdida, la probabilidad de una fundición sin defectos aumentará. Ahora, la función objetivo puede escribirse como:

(5)

2.4 Optimización del rango de parámetros del molde

Las restricciones de las funciones descritas en la tabla 2 se consideran aceptables porque derivan de resultados prácticos. Igual es el caso de los parámetros que definen las funciones mostradas en la tabla 1: están restringidos dentro de un rango de acuerdo con la información disponible en la literatura y las hojas de datos de la industria (Kulkarni y Babu, 2001, 2003, 2005), según se especifican en la tabla 3. Sin embargo, de acuerdo con los fines del proceso de optimización de este trabajo, es necesario buscar un método que permita optimizar aún más este rango de parámetros. En este sentido, con los rangos de valores de la tabla 3 y las funciones de la tabla 1, se diseñó un procedimiento heurístico utilizando el software Fortran 90, con la finalidad de optimizar los rangos de los parámetros para un proceso de producción de palanquillas de acero 20CrMnTi de sección transversal 269 x 269 mm. El procedimiento consistió en fijar una velocidad de colada con un valor muy alto, luego se ejecutó el comando random para asignarle de manera aleatoria a cada parámetro un valor dentro de su rango, y se procedió a calcular cada una de las funciones. Este proceso se ejecutó 10 000 veces. El programa descartaba aquella corrida en la que no se cumplieran todas las restricciones asignándole una métrica de cero (0), y donde sí se cumpliera se almacenaba y se le asignaba uno (1). Al finalizar la ejecución del programa, se mostraba en pantalla la suma de los escenarios que cumplían con las restricciones establecidas. Este procedimiento se realizó variando la velocidad de colada, para determinar a qué velocidad se cumplía el mayor grado de conformidad. Definida la velocidad de colada (la cual fue 1,11 m/min), se ejecutó el programa para determinar el valor inferior y superior de cada parámetro, los cuales eran almacenados mientras la corrida era considerada como válida. Los nuevos parámetros del proceso se muestran en la tabla 4.

Tabla 3
Rango de parámetros

Fuente: Kulkarni y Babu (2001, 2003, 2005), Venkata et. al (2014)

Tabla 4
Nuevos ajustes de los rangos de parámetros

Elaboración propia

2.5 Determinación del valor mínimo de la función objetivo

En este paso se utilizó una metaheurística basada en la optimización por cúmulos de partículas (PSO), para encontrar la mejor solución o, al menos, una solución lo suficientemente buena para el problema en estudio. El PSO fue introducido por Kennedy y Eberhart en 1995, quienes desarrollaron métodos simples que permitían optimizar eficientemente funciones matemáticas no lineales. El PSO fue inspirado en el comportamiento social del vuelo de las bandadas de aves o el movimiento de los bancos de peces, y se fundamenta en los factores que influyen en la toma de decisión de una partícula que forma parte de un conjunto de partículas similares. La toma de decisión por parte de cada partícula se realiza conforme a una componente social y una componente individual, y con base en esto se determina el movimiento (dirección) de la partícula, alcanzando una nueva posición en el espacio de soluciones (Kennedy y Eberhart, 1995; Kennedy et al., 2001). La componente individual puede modificar su opinión dependiendo de: su conocimiento sobre el entorno (su valor de fitness), su conocimiento histórico o experiencias anteriores (su memoria o conocimiento cognitivo), y el conocimiento histórico o experiencias anteriores de los individuos situados en su vecindario (su conocimiento social). La partícula actualiza su posición según (6):

(6)

Donde es la posición futura o bien la posición actualizada, representa la posición de la partícula en el instante de tiempo es la velocidad actualizada de la partícula . La figura 2 muestra el movimiento de la partícula.

Figura 2. Movimiento de una partícula en el espacio de soluciones

Fuente: García (2006)

Debido a que el vector velocidad se modifica teniendo en cuenta su experiencia y la de su entorno, en (7) se describe este comportamiento:

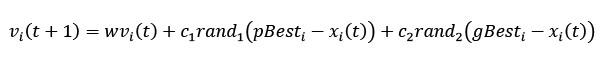(7)

Donde representa el factor de inercia que representa el grado de influencia de la velocidad actual sobre la velocidad futura, los factores y son constantes de aceleración cognitiva y social, que determinan en qué medida influyen sobre el movimiento de la partícula su propia memoria y la cooperación entre individuos, respectivamente; y son dos números aleatorios uniformemente distribuidos entre 0 y 1 cuyo objetivo es emular el comportamiento estocástico y un tanto impredecible que exhibe la población del enjambre, y representa la posición de la mejor solución encontrada por todo el cúmulo. El valor del factor inercia está dado por (7) según se muestra a continuación (Gutiérrez et al., 2017).

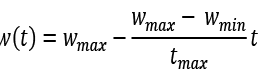(8)

Donde y son los valores máximo y mínimo de , es el número máximo de iteraciones. Luego de definir las expresiones matemáticas que fundamentan el PSO, en la figura 3 se muestra el diagrama de flujo que describe el algoritmo desarrollado en esta investigación. El proceso inicia en la llamada “población inicial”, que no es más que la generación aleatoria de los primeros valores de los parámetros del molde, manteniendo las nuevas restricciones de la tabla 4. También se calcula cada función de la tabla 1, las respectivas funciones de pérdida de la tabla 2, la función de pérdida total mostrada en (4), la mejor posición individual de cada parámetro , la mejor posición del grupo , y un valor de velocidad generado aleatoriamente entre 0 y 1. Con la información de la etapa de población inicial, se comienza el proceso de iteración del algoritmo. En la iteración 1, se actualiza la velocidad y posición de los parámetros del molde, con (7) y (6) respectivamente. Se calcula cada función de la tabla 1 y las respectivas funciones de pérdida de la tabla 2. En este primer ciclo, con el apoyo de (5) se espera que la función de pérdida total disminuya respecto al reportado en la etapa de población inicial, y esto se logra al encontrar las posibles combinaciones en las magnitudes de los parámetros del molde que minimicen la función de pérdida total. El ciclo termina con el cálculo de la mejor posición individual de cada parámetro y la mejor posición del grupo . El algoritmo continuará con el proceso de iteración (según haya sido programando), hasta observar que: (a) el factor de pérdida total no cambie respecto a las iteraciones anteriores, y (b) el factor de pérdida total sea el mínimo encontrado en todo el ciclo de iteraciones.

Figura 3. Diagrama de flujo del Particle Swarm Optimization (PSO)

Fuente: Gutiérrez et al. (2017)

3. RESULTADOS Y DISCUSIÓN

Con la finalidad de obtener un mínimo en la función objetivo que garantice una colada con la menor cantidad de defectos en el acero, se desarrolló un algoritmo heurístico que utiliza la técnica de Optimización por Enjambre de Partícula. El estudio se formuló como un problema de optimización multicriterio, utilizando las restricciones y modelos matemáticos mostrados en las tablas 1, 2 y 4; y la formulación de función de pérdida total fue del tipo minimización. La configuración se estableció con una población de 1000 para cada parámetro del molde, un máximo de iteraciones de treinta y una velocidad de colada de 1,11 m/min. Luego, la velocidad de colada fue variada en pequeñas magnitudes hasta obtener el valor más bajo en la función de pérdida total. Los valores optimizados de los parámetros del molde se alcanzaron a una velocidad de colada 1,03 m/min según se muestran en las tablas 5 y 6.

Tabla 5
Parámetros del proceso de colada continua de acero

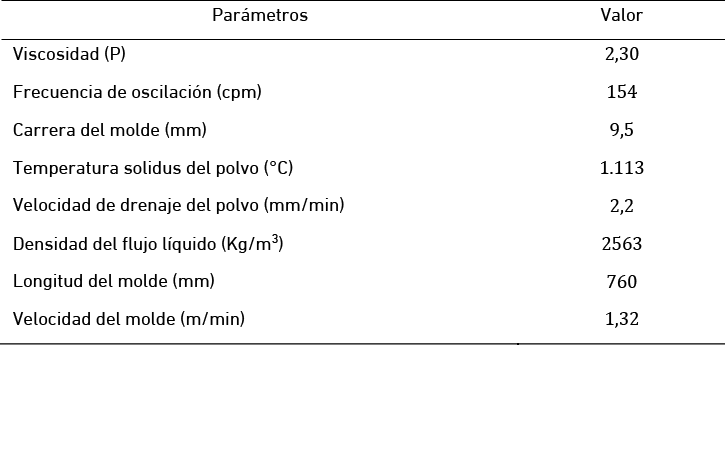
Elaboración propia

Tabla 6
Resultados del algoritmo PSO para la colada continua

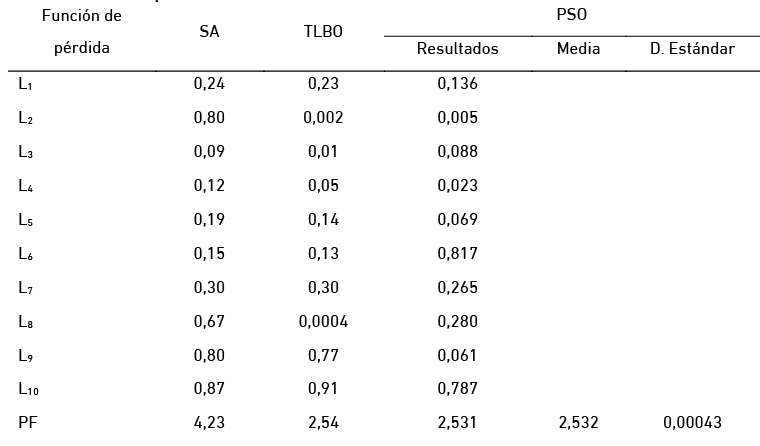Elaboración propia

Figura 4. Variación de la función de pérdidas total en el algoritmo PSO

Elaboración propia

Se puede observar en la tabla 5 que los parámetros del molde que se han optimizado por PSO están dentro de los límites que previamente fueron ajustados según el reporte de la tabla 4; además, están dentro de los límites propuesto por (Kulkarni y Babu, 2001, 2003, 2005), manteniendo las restricciones de la tabla 3. Respecto a las funciones de pérdida individual de la tabla 6, se observa una mejora considerable en todos los resultados del PSO respecto a los publicados por Venkata et al. (2014), sobre un proceso de optimización por recocido simulado (SA), excepto en la función L6. Y al comparar los resultados del PSO respecto al TLBO (Venkata et al., 2014) hubo una mejora en seis de las diez condiciones. En las funciones individuales donde hubo mejoras, en general la indeseabilidad se aproximó a cero, sin embargo la mejoría en L7 y L10 no fue tan importante. Este comportamiento en los resultados obedece a que en las funciones de pérdida existen parámetros comunes y se debe cumplir con las restricciones descritas en las tablas 1 y 3, simultáneamente.

El algoritmo PSO ha dado una mejora mínima respecto al TLBO en la función de pérdida total, logrando disminuir de 2,54 (en el TLBO) a 2,531, lo que representa un porcentaje muy pequeño, pero no deja de ser importante. El promedio de la función de pérdida total en el PSO con 50 corridas fue de 2,532, valor que es muy aproximado a la mejor solución, con una desviación estándar de 0,00043, lo que permite afirmar que desde un punto de vista estadístico la dispersión es mínima. En la figura 4 se observa cómo el PSO alcanzó la convergencia de los resultados, según los resultados publicados por Venkata et al. (2014), el PSO alcanzó mucho más rápido la mejor solución respecto al TLBO, solo hizo falta cerca de 20 iteraciones para llegar al mínimo, en este sentido el tiempo de cálculo es mucho menor con el PSO que con el TLBO. Sin duda el PSO representa una herramienta útil para mejorar el rendimiento de plantas de colada continua.

4. CONCLUSIONES

En este artículo se ha desarrollo un algoritmo basado en cúmulos de partículas (Particle Swarm Optimization, PSO), que simula el comportamiento social del vuelo de las bandadas de aves o el movimiento de los bancos de peces para determinar los parámetros del molde de un proceso de colada continua de acero que más se ajuste a una fundición sin defectos. El PSO ha manejado efectivamente diversos modelos matemáticos y ha demostrado buenas capacidades en el campo de la optimización de parámetros que influyen en el proceso de colada continua. En el proceso de colada continua el algoritmo PSO arrojó, en seis de las diez condiciones de funciones de pérdidas individuales, valores más bajos que los arrojados por el algoritmo optimización de enseñanza-aprendizaje TLBO. El algoritmo PSO disminuyó la función de pérdida total a 2,531, lo que es una mejora muy pequeña con respecto a los resultados del TLBO (2,54), pero importante. Con el PSO la convergencia de los resultados se alcanzó cerca de las diecisiete iteraciones, mientras que con el TLBO fueron necesarias más de treinta iteraciones para estabilizar el total de funciones de pérdida. El algoritmo PSO desarrollado tiene un alto potencial para gestionar la calidad en el sistema de colada continua, sin embargo, se recomienda aplicar en otros tipos de procesos de fundición que no han sido estudiados en esta investigación.

REFERENCIAS

Aballe, M. (1992). Colada continua y semicontinua de productos industriales, Conference:
2.ª Jornada de Ciencia y Tecnología de Materiales. Barcelona.

Adilson, J. Amaral, B. Sampaio, R. Mendes, E., y Leão, I. (9 de abril del 2018) Numerical Study of Turbulent Flows and Heat Transfer in Coupled Industrial-Scale Tundish of a Continuous Casting Material in Steel Production, Numerical Simulations in Engineering and Science, Srinivas P. Rao, IntechOpen, doi: 10.5772/intechopen.75935.

Bäck, T, Fogel, D., y Michalewicz, Z. (1997). Handbook of Evolutionary Computation. IOP Publishing and Oxford University Press.

Belisario, J. (2011). Evaluación de la efectividad del proceso de colada en la reducción de defectos de salpicaduras en las palanquillas producidas en la acería 150 TM de Sidor. [Tesis de grado en ingeniería industrial. Universidad Nacional Experimental de Guayana].

Calvo, J. (2006). Efecto de los elementos residuales e impurezas en la ductilidad y mecanismos de fragilización en caliente de un acero de construcción 0,23C – 0,9Mn – 0,13Si. [Tesis Doctoral, UPC].

Chang, V., y Bolsaitis, P. (1982). Simplified Model for Heat Transfer and Solidification in Continuous Casting, Latin American Journal of Metallurgy and Materials, 2(2).

Cicutti, C. (1977). Transferencia de calor en la colada continua de aceros, I parte, el molde. Metalurgia, pp. 333-344.

Coley, J. (2010). Fundición continua, una oportunidad para mejorar la calidad de los hierros. Revista metalactual.com. Procesos, pp. 10-17.

Concast Data Sheets. (1992). Specification distribution sheets for thermal modelling, Concast (I) Ltd.

Cruz, A. Hernández, O. Moreno, A., y Vargas, M. (2007). Caracterización de fundentes para molde de colada continua de acero. Acta Universitaria, 17(1), enero-abril, Universidad de Guanajuato, pp. 52-58.

Dorigo, M. (2000). The Ant Colony Optimization Metaheuristic: Algorithms, Applications and Advances. Technical Report IRIDIA-2000-32, Université Libre de Bruxelles, IRIDIA.

Feng, Y. Wu, M. Chen, X. Chen, L., y Du, S. (2020). A Fuzzy PID Controller with Nonlinear Compensation Term for Mold Level of Continuous Casting Process. Information Sciences 539, 487-503.

Flores, B. (2010). Descripción del proceso de colada continua mediante CFD. [Tesis de maestría en ciencias de la ingeniería mecánica con especialidad en materiales, Universidad Autónoma de Nuevo León].

García, J. (2006). Algoritmos Basados en Cúmulos de Partículas Para la Resolución de Problemas Complejos. Departamento de Lenguajes y Ciencias de la computación. Universidad de Málaga.

García Nieto, P. J., García-Gonzalo, E., Álvarez Antón, J. C., González Suárez, V. M., Mayo Bayón, R., y Mateos Martín, F. (2018). A Comparison of Several Machine Learning Techniques for the Centerline Segregation Prediction in Continuous Cast Steel Slabs and Evaluation of its Performance. Journal of Computational and Applied Mathematics, 330, 877-895.

Gutiérrez, D. Villa W., y López, J. (2017). Flujo óptimo reactivo mediante optimización por enjambre de partículas. Información Tecnológica, 28(5), 215-224.

Hahn, I. Schneider, M. Terhaar, J. Jarolimeck, J., y Sauermann, R. (2012). Quality Prediction of Cast Ingots. 1 International Conference on Casting, Rolling and Forging ICRF.

Hernández, J. (1994). La calidad total, una utopía muy práctica. Universidad Pontifica Comillas.

Kennedy, J. y Eberhart, R. (1995). Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, volume 4, pp. 1942-1948.

Kennedy, J. Eberhart, R., y Shi, Y. (2001). Swarm Intelligence. San Francisco: Morgan Kaufmann Publishers.

Kulkarni, M. S., y Subash Babu, A. (2001). Metamodels for continuous casting, CARE Technical Report, Indian Institute of Technology.

Kulkarni, M. S., y Subash Babu, A. (2003). A System of Process Models for Estimating Parameters of Continuous Casting Using Near Solidus Properties of Steel, Mater. Manufact. Process, 18, 287-312.

Kulkarni, M. S., y Subash Babu, A. (2005). Managing Quality in Continuous Casting Process Using Product Quality Model and Simulated Annealing. J. Mater. Process. Technol. 166, 294-306.

Kumar, R. (2015). Computational Fluid Dynamic (CFD) simulation for continuous casting process of steels. [Master of Technology in Metallurgical and Materials Engineering, National Institute of Technology Rourkela].

Kumar, S. (1996). Mould Thermal Response and Formation of Defects in the Continuous Casting of Steel Billets. [Degree Of Doctor Of Philosophy. The University Of British Columbia].

Lei, Z., y Su, W. (2019). Research and Application of a Rolling Gap Prediction Model in Continuous Casting. Metals, 9(3), 380.

Li, Y. R., y Zang, W. L. (2021). Prediction and Analysis of Slab Quality Based on Neural Network Combined with Particle Swarm Optimization (PSO). Metalurgija, 60(1-2), 15-18.

Luo, X. Xie, Q. Wang, Y., y Yang, C. (2017). Estimation of Heat Transfer Coefficients in Continuous Casting under Large Disturbance by Gaussian Kernel Particle Swarm Optimization Method. International Journal of Heat and Mass Transfer, 111, 1087-1097.

Mannheim, R. (1983). Introducción general a la colada continua. Revista Remetallica 5, 28-38.

Mills, K. Ramirez, P. Lee, P. Santillana, B. Thomas, B., y Morales, R. (2014). Looking into Continuous Casting Mould. Ironmaking & Steelmaking. Ironmaking and Steelmaking, 41(42).

Najera, A. (2010). Análisis del flujo de fluidos y transferencia de calor sobre la calidad de palanquillas de acero. [Tesis de grado de doctor en ciencias en metalurgia y materiales. Instituto politécnico nacional].

Rao, R. Savsani, V., y Vakharia, D. (2011). Teaching–Learning-Based Optimization: a Novel Method for Constrained Mechanical Design Optimization Problems, Comput. Aided Des. 43, 303-315.

Rao, R. Savsani, V., y Vakharia. D. (2012). Teaching–Learning-Based Optimization: an Optimization Method for Continuous Non-Linear Large Scale Problems, Inf. Sci. 183, 1-15.

Rao R., y Patel, V. (2012). An Elitist Teaching–Learning-Based Optimization Algorithm for Solving Complex Constrained Optimization Problems, Int. J. Ind. Eng. Comput. 3(4), 535-560.

Romo, J. (2009). Estudio de la formación de especies mineralógicas en el molde de colada continua de planchón delgado de acero. [Tesis de maestría en ciencias en ingeniería metalúrgica, Instituto politécnico nacional].

Saldaña, F. Torres, E. Ramos, J. Solorio, G., y Hernández, C. (2019). Analysis of the Depth of Immersion of the Submerged Entry Nozzle on the Oscillations of the Meniscus in a Continuous Casting Mold. Metals 9, 596.

SEMCCO. (2012). Lecture Notes in Computer Science, 7677, 540-547. https://doi.org/10.1007/978-3-642-35380-2_63

Stephan O., y Zomaya, A. (2005). Handbook Of Bioinspired Algorithms and Applications. CHAPMAN and HALL/CRC.

Venkata R., y Kalyankar, V. D. (2012). Parameters Optimization of Continuous Casting Process Using Teaching-Learning-Based Optimization Algorithm.. En Panigrahi B.K., Das S., Suganthan P.N. y Nanda P.K. (Eds.) Swarm, Evolutionary, and Memetic Computing. SEMCCO 2012. Lecture Notes in Computer Science, vol 7677, 540-547. https://doi.org/10.1007/978-3-642-35380-2_63

Venkata R. Kalyankar V. D., y Waghmare, G. (2014). Parameters Optimization of Selected Casting Processes Using Teaching–Learning-Based Optimization Algorithm. Applied Mathematical Modelling, 38, 5592–5608.

Wang, X. Wang, Z. Liu, Y. Du, F. Yao, M., y Zhang, X. (2016). A Particle Swarm Approach for Optimization of Secondary Cooling Process in Slab Continuous Casting. International Journal of Heat and Mass Transfer, 93, 250-256.

Wang, Y. Luo, X. Zhang, F., y Wang, S. (2019). GPU-Based Model Predictive Control for Continuous Casting Spray Cooling Control System Using Particle Swarm Optimization. Control Engineering Practice, 84, 349-364.

Wang, Z. Zhang, Y. Jiang, Y. Zhang, J., y Zhang, S. (2020). An Optimization Control Method for Heat Transfer Model during Slab Continuous Casting. Journal of Physics: Conference Series, 1575 012208.

Yang, J. Xie, Z. Meng, H. Liu, W., y Ji, Z. (2014). Multiple Time Steps Optimization for Real-Time Heat Transfer Model of Continuous Casting Billets. International Journal of Heat and Mass Transfer, 76, 492-498.

Yu, Y., y Luo, X. (2017). Identification of Heat Transfer Coefficients of Steel Billet in Continuous Casting by Weight Least Square and Improved Difference Evolution Method. Applied Thermal Engineering, 114, 36-43.

Zhang, X. Chen, W., y Zhang, L. (2017). A Coupled Model on Fluid Flow, Heat Transfer and Solidification in Continuous Casting Mold. China Foundry, 14(5).